因果推断导论笔记-Lecture2-Assignment Mechanism
分配机制的介绍。分配机制对因果推断非常重要。
一些记号
共五个元素:Unit,Treatment,Potential outcomes,X(协变量),W(分配)。
随机性来源于W,W是一个随机变量(可取0取1)。
分配机制,就是要研究
平均因果作用(ACE),average causal effect,定义为:
观测值、缺失值相当于一个复合的映射:
Simpson’s Paradox
New Jersey州的考试成绩比Nebraska的考试成绩低,但是分人种的话全部都是New Jersey州占优。
这是因为New Jersey州的白人占比比较少,而白人的平均成绩会比较高。
所以如果加权来看(用国家的人种比例统一加权),New Jersey州的成绩更好。
选择哪种计算方式,Depends on your questions。

人种在这里就是协变量,不是我们关心的因果变量。
因此可以看出分配机制不仅和潜在结果有关,还和协变量有关。
分配机制的精确定义
分配机制
分配机制是一个随机向量。有n个units,分配机制就是n维,共有种取值。

两种处理的协变量比例要相同。
倾向得分Propensity Score

相当于边缘概率的另外一个方向,一个子总体内部有多高的比例分配到处理组。
从另一个角度,倾向得分可以作更粗的划分,使得样本量增大。
通过例子理解


下面这个例子是更复杂的分配机制,unit1随机,unit2和unit1相反,unit3取决于哪个结果更好(不考虑结果相等):

进入某个平行世界后,Y就没有随机性了。分析过程可以先画序贯树:
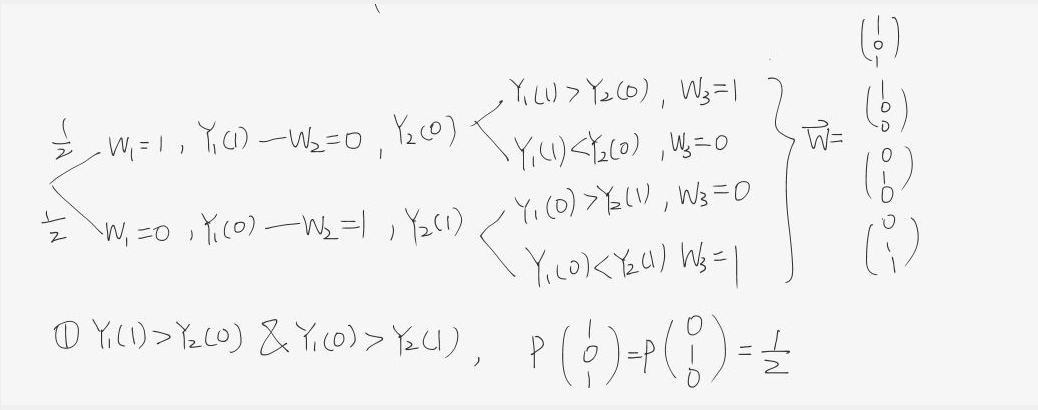
结果如下:

假设
从上面可以看出分配机制很复杂,需要增加一些假设来简化。
个体化假设
上述要取决于其他个体的潜在结果。
因此假设为:一个个体的分配概率和其他协变量、其他个体的潜在结果无关,且如果协变量、潜在结果相同,概率相同。还假设了向量的联合概率分布可以从边缘的概率表示。

这样,倾向得分化简为:
概率性分配
probabilistic.
简单来讲就是每一项倾向得分都要在(0, 1)之间。
无混杂假设
在Simpson悖论中,Y是通过影响X来影响W的,平衡了X,Y就没影响了。
因此假设在X条件下,W和Y独立。

这样,倾向得分就化简成了:
如果无混杂假设不成立怎么办?
可以尝试增加X,使其达到无混杂。
但是也不是所有X都加进来,有可能多加一个X就不独立了。
以上三种假设称为强可忽略性假设。
普通的可忽略性假设指的是,分配机制可以不依赖于看不到的了,只取决于。
上面三条假设和SUTVA没有直接的强弱关系,SUTVA是在客观的没有随机性的世界里的假设,而上述三条假设是在分配机制上的假设。但有关联,因为是在SUTVA的基础上完成的。
两种data collection
Randomized Experiments
an assignment mechanism that
- is probabilistic, and
- has a known functional form that is controlled by the researcher.
经典的随机化试验还要求:
- individualistic and
- unconfounded
经典随机化试验有四种特例,区别就是支撑集(真实可能取到的集合):
Bernoulli Trails
按概率独立地随机抽:

Completely Randomized Experiment
数量要固定:

此外还有Stratified Randomized Experiment和Paired Randomized Design。
Observational
the functional form of the assignment mechanism is unknown(the key difference from experiments).
要求是规则的,即满足:
- individualistic
- probabilistic
- unconfounded