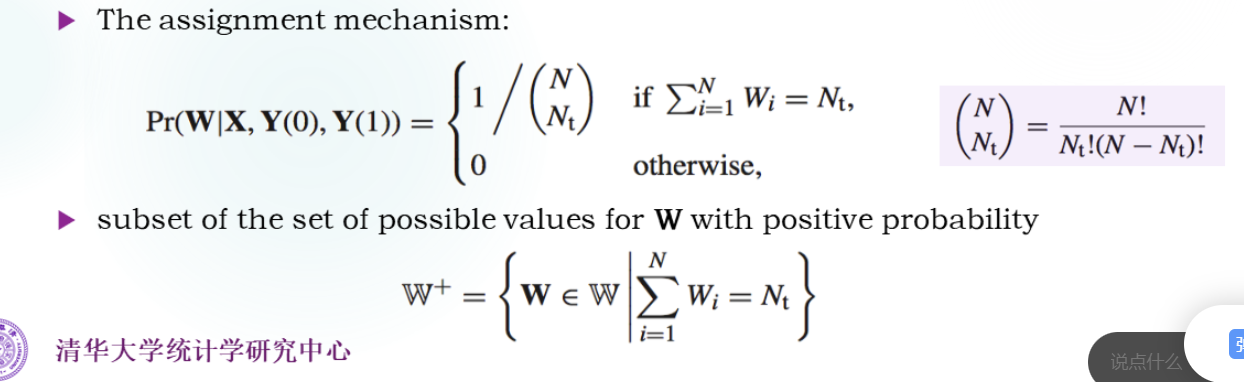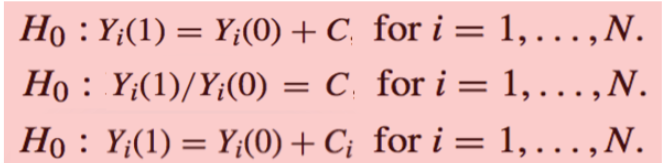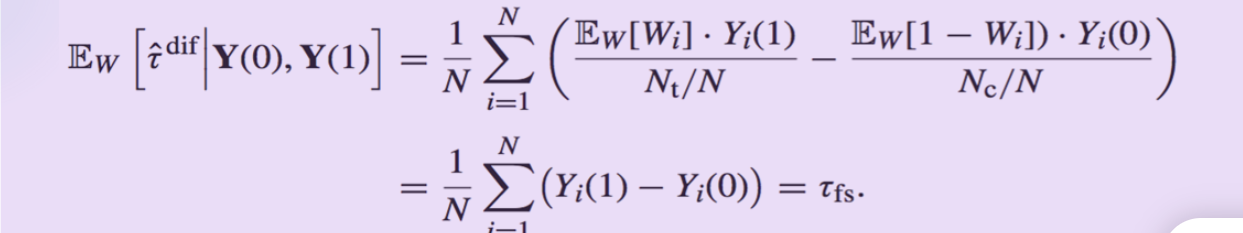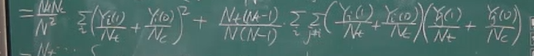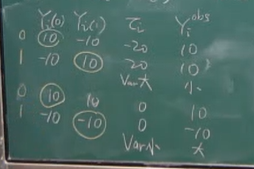本课针对的是完全随机化试验。
完全随机化试验
Completely Randomized Experiments :
N t N_t N t N t N_t N t N c N_c N c
Fisher’s Exact P-value ( FEP )
本质上是非参 的方法,选择统计量有较高的自由度。
需要解决缺失数据的问题。
平均因果作用的假设是H 0 : τ f s = 0 H_0: τ_{fs}=0 H 0 : τ f s = 0 H 0 : Y i ( 0 ) = Y i ( 1 ) H_0: Y_i(0)=Y_i(1) H 0 : Y i ( 0 ) = Y i ( 1 )
统计量Stat:T ( W , Y o b s ) = T d i f = ∣ Y ˉ t o b s − Y ˉ c o b s ∣ T(W,Y^{obs})=T_{dif}=|\bar{Y}_t^{obs}-\bar{Y}_c^{obs}| T ( W , Y o b s ) = T d i f = ∣ Y ˉ t o b s − Y ˉ c o b s ∣
枚举所有可能的W,然后算每一种W的T d i f T_{dif} T d i f
零假设
零假设的构造方法有很多种:
统计量
选择合适的统计量,看功效,下图这些都是非参的。
下面是两个参数的,和一个非参的。参数比非参在合适范围内的功效更高。
参数模型给错了,FEP方法还有效吗?(先不谈功效)
还是有效的。算出来的P值还是对的,也能算出统计量,只是功效可能很小。
P值的计算
组合数是非常庞大的。
我们是要求P ( T > T o b s ) = E 1 { T > T o b s } P(T>T^{obs})=E\bold{1}_{\{T>T^{obs}\}} P ( T > T o b s ) = E 1 { T > T o b s }
由大数定律,可以采样来估计这个值:
p ^ = 1 K ∑ k = 1 K 1 T d i f , k ≥ T d i f , o b s \hat{p}=\frac{1}{K}\sum_{k=1}^{K}\bold{1}_{T^{dif,k}≥T^{dif,obs}}
p ^ = K 1 k = 1 ∑ K 1 T d i f , k ≥ T d i f , o b s
由中心极限定理CLT,方差为p ∗ ( 1 − p ∗ ) / K ≤ 1 / 2 K \sqrt{p^*(1-p^*)/K}≤1/2\sqrt{K} p ∗ ( 1 − p ∗ ) / K ≤ 1/2 K
局限性
协变量X没有参与
点估计τ ^ \hatτ τ ^
扩展
引入协变量
还可以用除法,或者回归:
CI有三种,称为BFF:
τ∈[1.0 , 3.8],置信区间confidence I,也就是区间是动的,100次实验有95%次能覆盖真实的τ。这是频率学派。
τ∈[1.0 , 3.8],可信区间credible I,也就是τ是动的,而区间是定的。这是贝叶斯学派。
H 0 : Y i ( 1 ) = Y i ( 0 ) + C H_0:Y_i(1)=Y_i(0)+C H 0 : Y i ( 1 ) = Y i ( 0 ) + C
Neyman’s approach
Goal: τ f s = 1 n ∑ i = 1 N ( Y i ( 1 ) − Y i ( 0 ) ) τ_{fs}=\frac1n\sum_{i=1}^N(Y_i(1)-Y_i(0)) τ f s = n 1 ∑ i = 1 N ( Y i ( 1 ) − Y i ( 0 ))
Estimatior:τ d i f = Y ˉ t o b s − Y ˉ c o b s τ^{dif}=\bar{Y}^{obs}_{t}-\bar{Y}^{obs}_{c} τ d i f = Y ˉ t o b s − Y ˉ c o b s
τ d i f = ∑ i = 1 N W i Y i ( 1 ) N t − ∑ i = 1 N ( 1 − W i ) Y i ( 0 ) N c τ^{dif}=\frac{\sum_{i=1}^{N}W_iY_i(1)}{N_t} - \frac{\sum_{i=1}^{N}(1-W_i)Y_i(0)}{N_c}
τ d i f = N t ∑ i = 1 N W i Y i ( 1 ) − N c ∑ i = 1 N ( 1 − W i ) Y i ( 0 )
是一个无偏估计:
区间估计
先找方差的理论值。
直观上,V a r W ( τ ^ d i f ) Var_W(\hatτ^{dif}) Va r W ( τ ^ d i f )
V a r ( τ ^ d i f ) = V a r ( ∑ i Y i + W i ) Var(\hatτ^{dif})=Var(\sum_iY_i^+W_i)
Va r ( τ ^ d i f ) = Va r ( i ∑ Y i + W i )
令D i = W i − E W i D_i=W_i-EW_i D i = W i − E W i
= E [ ( ∑ i Y i + D i ) 2 ] = ∑ i ( Y i + ) 2 E ( D i 2 ) + ∑ i ∑ j ≠ i Y i + Y j + E ( D i D j ) =E[(\sum_{i}Y_i^+D_i)^2]\\
=\sum_i(Y_i^+)^2E(D_i^2)+\sum_i\sum_{j≠i}Y_i^+Y_j^+E(D_iD_j)
= E [( i ∑ Y i + D i ) 2 ] = i ∑ ( Y i + ) 2 E ( D i 2 ) + i ∑ j = i ∑ Y i + Y j + E ( D i D j )
其中E ( D i 2 ) = V a r ( W i ) = N t N c N 2 E(D_i^2)=Var(W_i)=\frac{N_tN_c}{N^2} E ( D i 2 ) = Va r ( W i ) = N 2 N t N c
E ( W i W j ) = P ( W i = 1 , W j = 1 ) = N t N N t − 1 N − 1 E(W_iW_j)=P(W_i=1,W_j=1)=\frac{N_t}{N}\frac{N_t-1}{N-1} E ( W i W j ) = P ( W i = 1 , W j = 1 ) = N N t N − 1 N t − 1
E ( D i D j ) = E ( W i W j ) − E ( W i ) E ( W j ) = N t N ( N t − 1 N − 1 − N t N ) = − N t N c N 2 ( N − 1 ) E(D_iD_j)=E(W_iW_j)-E(W_i)E(W_j)=\frac{N_t}{N}(\frac{N_t-1}{N-1}-\frac{N_t}{N})=-\frac{N_tN_c}{N^2(N-1)} E ( D i D j ) = E ( W i W j ) − E ( W i ) E ( W j ) = N N t ( N − 1 N t − 1 − N N t ) = − N 2 ( N − 1 ) N t N c
分解的结果:
Neyman假设了S t c 2 S_{tc}^2 S t c 2
Y(1)和Y(0)正相关,估计的方差更大。
直观上分析,我们只能观测到部分数据,看这个图就知道了。
推导:
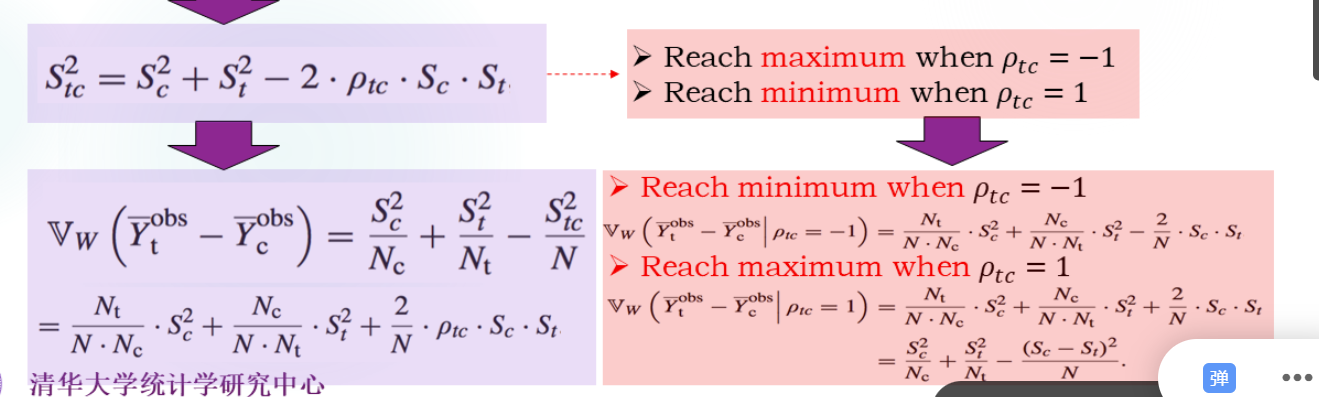
方差的两种优化以及置信区间
方差相等的情况 :
这是假设所有个体的因果效应一致,那么S t c S_{tc} S t c
用相关系数来表示:
上面两种情况都是精确的计算公式,S t S_t S t S c S_c S c S t S_t S t S c S_c S c S t c , ρ t c S_{tc},ρ_{tc} S t c , ρ t c Y i ( 0 ) Y_i(0) Y i ( 0 ) Y i ( 1 ) Y_i(1) Y i ( 1 )
如果S t 2 = S c 2 S_t^2=S_c^2 S t 2 = S c 2
注意下面全换成V ^ \hat{V} V ^
对相关系数进行放缩
估计
前文小写是分配机制后的,大写是上帝视角的,但这里又换了过来
很奇怪,因为觉得大写的才是“样本的”,才是分配机制后的才对啊。。。
有时间把过程补上:
E W ( S t 2 ) = E [ 1 N t − 1 ∑ i W i ( Y i ( 1 ) − Y ˉ t o b s ) 2 ] = s t 2 E_W(S_t^2)=E[\frac1{N_t-1}\sum_iW_i(Y_i(1)-\bar{Y}_t^{obs})^2]=s_t^2
E W ( S t 2 ) = E [ N t − 1 1 i ∑ W i ( Y i ( 1 ) − Y ˉ t o b s ) 2 ] = s t 2
置信区间
方差估计的总结
valid是指需要达到名义上的α,比如,至少覆盖住“95%”。
effective是指相同α下CI尽可能短:
为什么这里第二个说更精确呢?因为这里s是pooled了的,样本更大。
两种方法的检验