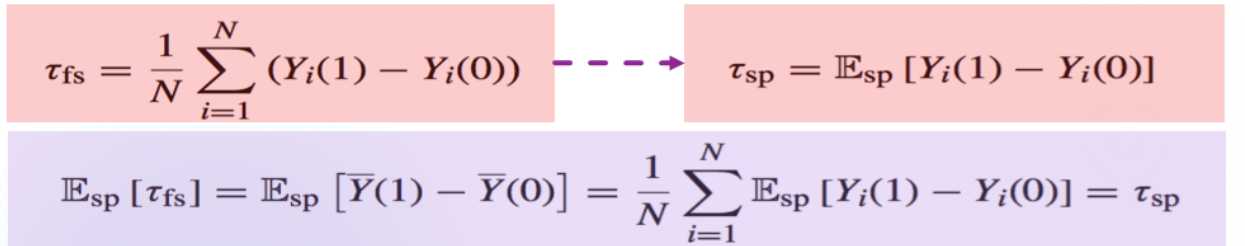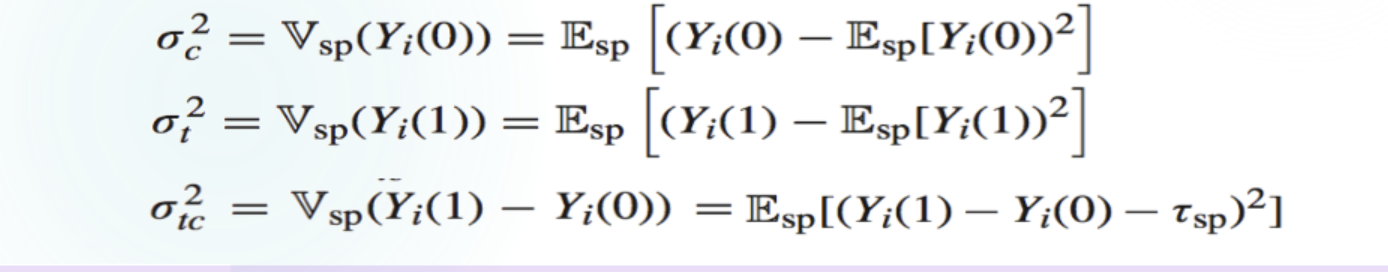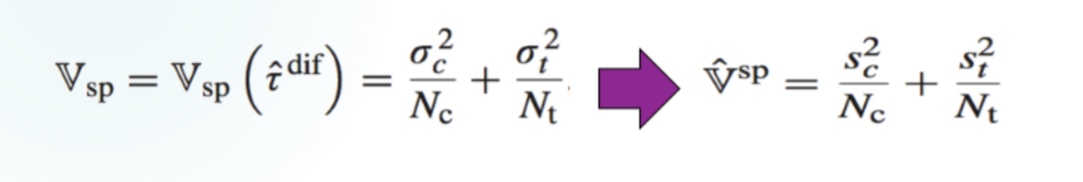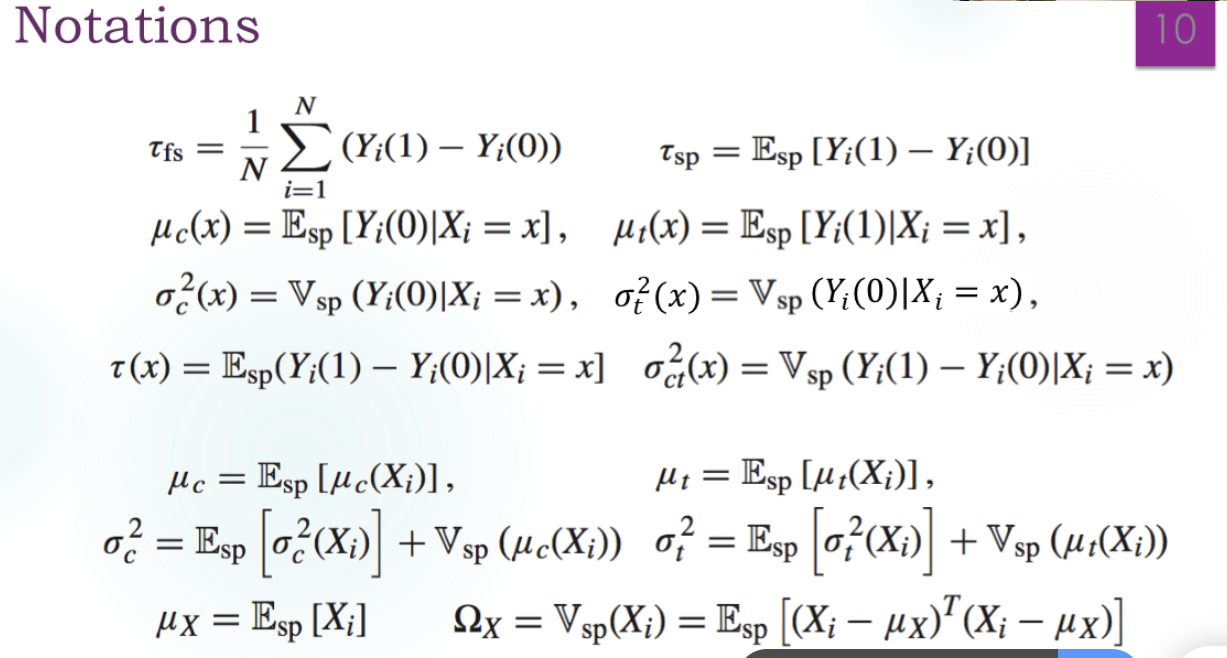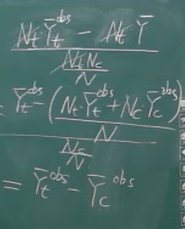今天的目标是有限->无限,以及引入协变量。
概念
真正关心的可能是super population(近似无限)的因果作用,数据只是i.i.d.抽取出来的子总体而已。

The casual estimand for a super population is(注意和τfs的区别)
τsp=Esp[Yi(1)−Yi(0)]
Y从没有随机性到有随机性,和之前课程的区别是:这个式子里的Yi(1)是有随机性的,这个随机性来源于抽样,而不是映射。
现在随机性有两层,τsp到τfs中的期望是E(Y,X),而τfs到最后的因果作用是EW
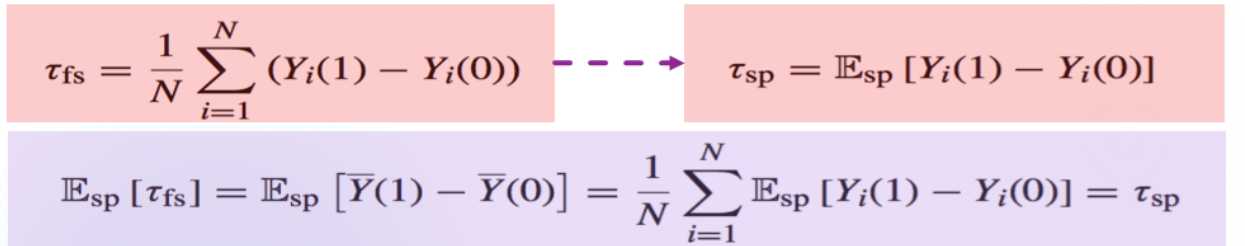
对于上次课定义的τ^dif,仍然是无偏的(利用重期望公式,先选定人群):
E(τ^dif)=Esp[EW(τ^dif∣Y)]=Esp[τfs]=τsp
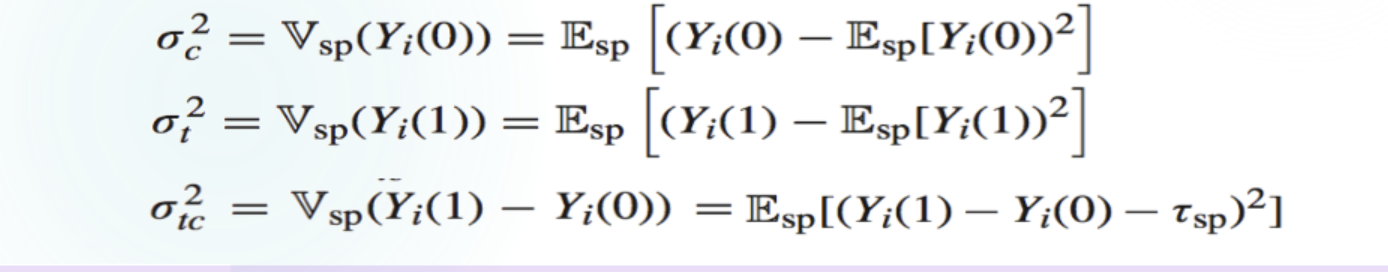
Vsp(τfs)=Vsp(N1∑(Yi(1)−Yi(0)))=N21∑Vsp(Yi(1)−Yi(0))=N1σtc2
V(τ^dif)=E(τ^dif−τsp)2(因为是无偏的)=E(τ^dif−τfs+τfs−τsp)2
详细推导如下:

交互项这么算:
E[(τ^dif−τfs)(τfs−τsp)]=Esp[EW[(τ^dif−τfs)(τfs−τsp)∣Y]]=Esp[(τfs−τsp)EW[(τ^dif−τfs)∣Y]]=Esp[(τfs−τsp)EW[(τ^fs−τfs)∣Y]]=0
(第二个等号能拿出来,因为那两个量和分配机制W无关,只和抽样Y有关。)
所以结果是
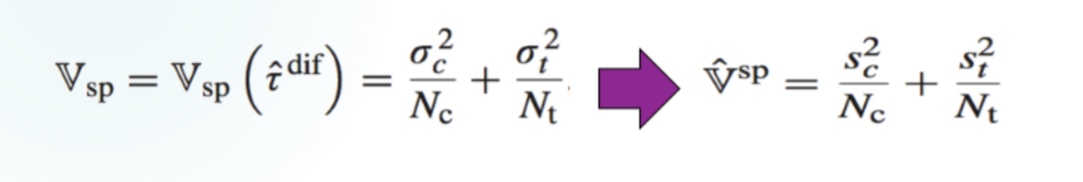
是Neyman估计的结果
为什么在有限总体里Neyman估计较为保守,而无限总体是无偏的?
因为无限总体多了抽样这种变异性,所以方差要更大一点。
回归模型
如何利用协变量改进估计(减小方差)?
记号
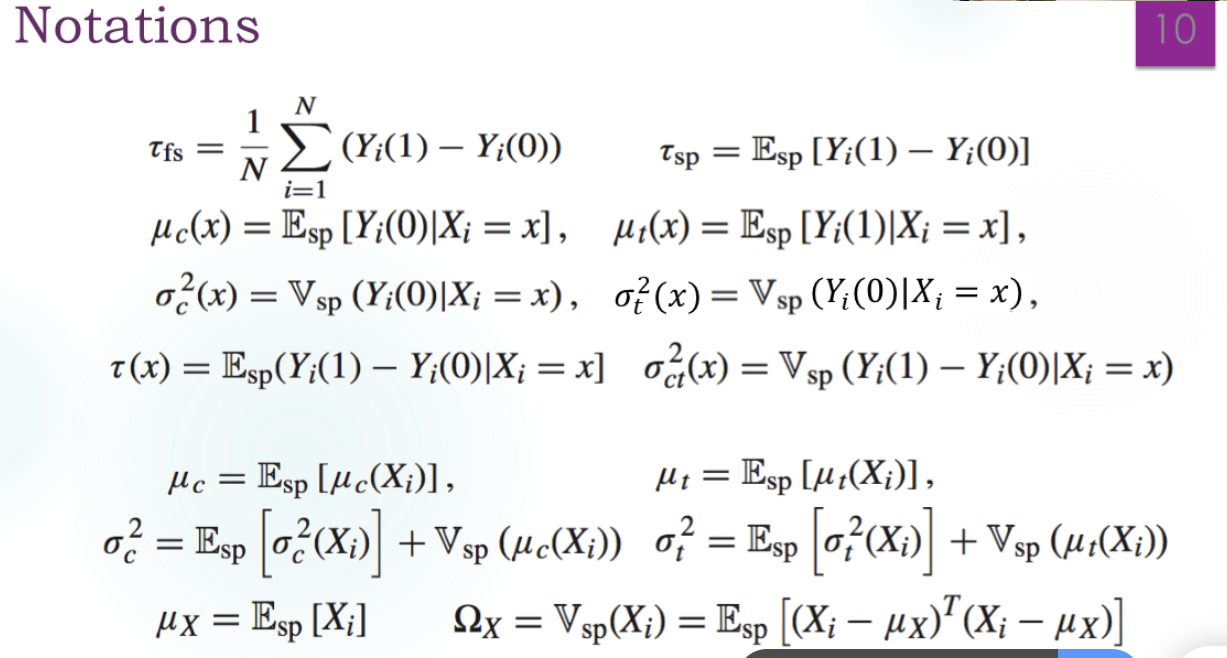
模型

这个τ有没有因果意义呢?
化简一下:
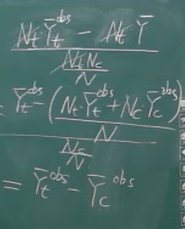
结果如下,就是τ^dif:

而α^obs=Yˉcobs
也就是说Wi=0时,回归的结果是α=Yˉcobs加一个误差。Wi=1时,回归的结果是α+τ=Yˉtobs加一个误差。
是否符合传统的线性回归?
Yi(1)=EspYi(1)+εi=α+τ+εi
Yi(0)=EspYi(0)+εi=α+εi
我们的模型没有任何附加假设,只是做了一个形式的转换。
线性回归的假设是:ε零均值,同方差,和X独立。

而
Cov(Wi,εi)=E(Wiεi)−0=E[E(Wiεi∣Wi)]=0
因此,这是一个合格的回归模型。
理解方式
第一种理解方式——Neyman方法



第二种理解方式——填补

算出来就是τ^dif:
N1i=1∑Nτ^i=N1(i:Wi=1∑N(Yi(1)−Ycˉobs)+i:Wi=0∑N(Ytˉobs−Yi(0)))=N1(NtYtˉobs−NtYcˉobs−NcYcˉobs+NcYtˉobs)=τ^dif
第三种理解方式——极限

最后一步是因为无混杂假设,E(Yi(1)∣Wi=1)=E(Yi(1))
如何引入X?
对于第三种理解:
把εi拆成(Xi−μX)β+ε~i,多减一个μX是为了保证后面期望为0


推理完全没有要求X和Y是线性关系。
引入了X,方差比Neyman估计小了。

相当于比较σY2和σY∣X2
利用全方差公式:
Var(Y)=E(Var(Y∣X))+Var(E(Y∣X))