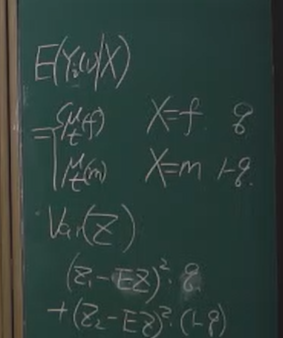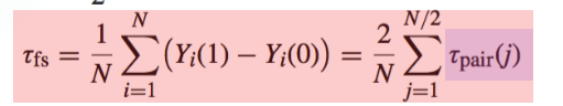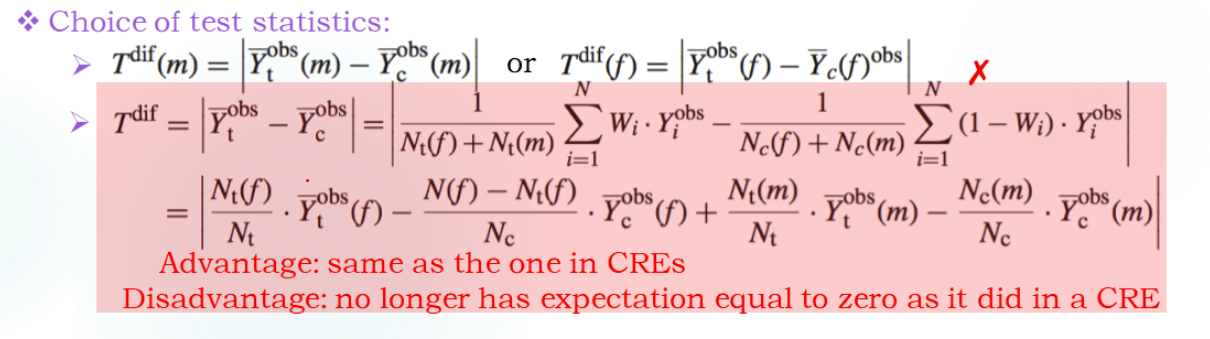因果推断导论笔记-Lecture6-Stratified & Pairwise Randomized Experiments

分层是为了防止整体把某些因果作用掩盖了。配对，例如双胞胎，是分层的特例，分得特别细。

分层随机化试验

重点是Neyman和回归方法

记号

j是分层的某一层，例如16个学校。

$N_c(j)$和$N_t(j)$分别是第j层的控制组个数和处理组个数、

倾向得分：$e(j)=\frac{N_t(j)}{N(j)}$

分层的比例：$q(j)=N(j)/N$（横向的比较）

满足无混杂假设：$P(W|X,Y)=P(W)$

本课考虑分两层的情况：

Fisher方法下，如何填补？

Is $T^{dif}=|\bar{Y_t}^{obs}-\bar{Y_c}^{obs}|$ still valid?

Yes. 理论上可以得到真分布，是对W的重排。Fisher方法用什么统计量都可以（

Is $\bar{Y_t}^{obs}-\bar{Y_c}^{obs}$ still unbiased?

No。取决于倾向得分。

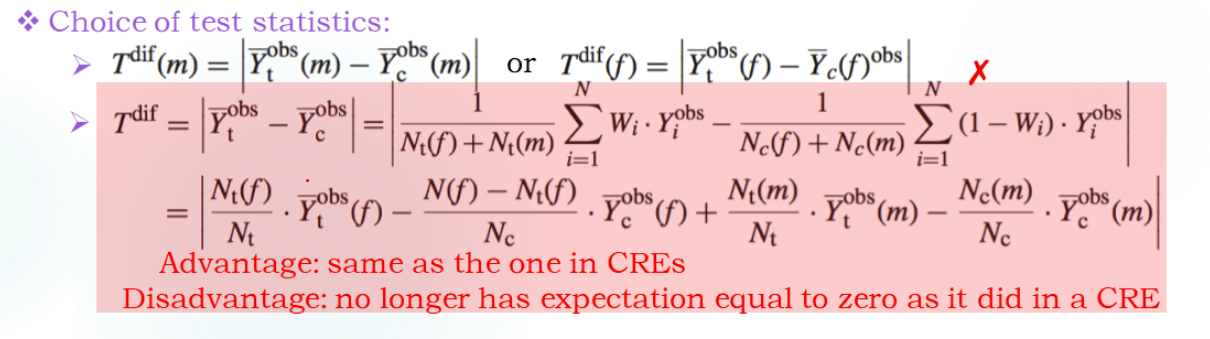
加权的计算是可以的，而如果使用秩也需要加权：

Neyman方法

SREs vs CREs

W(竖表)X(横表)	f	m
0	$N_c(f)$	$N_c(m)$
1	$N_t(f)$	$N_t(m)$

$q = N(f)/N$

假设$e(j)=N_t(j)/N(j)=p=N_t/N$

$$σ^2_t=Var(Y_i(1))=E[Var(Y_i(1)|X)]+Var[E(Y_i(1)|X)]$$

CRE到SRE，精度提高了（方差变小了）。从图中式子可以看到，不同组之间的差异越大，分组的效果越好。也就是说无论协变量分层有没有用，精度至少不会降低。（但也不是说一味地添加协变量越好，因为实际上方差是要估计的，分层越细样本量越小）

精确的计算**( 要求掌握，复习的时候注意推一下 )**（见下方）：

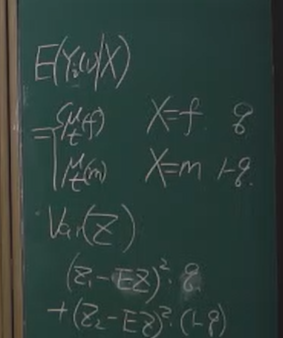
两点分布（设X=1为男，X=0为女）的特性得到：

$$Var[E(Y_i(1)|X)]=Var[Xμ_t(f)+(1-X)μ_t(m)] \\=Var[X(μ_t(f)-μ_t(m))] \\=q(1-q)[μ_t(f)-μ_t(m)]^2$$

$$E[Var(Y_i(1)|X)]=qσ_t^2(f)+(1-q)σ^2_t(m)$$

故：

$$σ^2_t=qσ_t^2(f)+(1-q)σ^2_t(m)+q(1-q)[μ_t(f)-μ_t(m)]^2$$

所以：

$$NV_{sp}(\hatτ^{dif})=N(\frac{σ_c^2}{N_c}+\frac{σ_t^2}{N_t}) \\=\frac{σ_c^2}{1-p}+\frac{σ_t^2}{p}$$

和$NV_{sp}(\hatτ^{strat})$相减就可以消去很多项。

回归方法

β(j)是第j层的截距。用了截距可以不同，斜率要相同的回归模型。

$w(j)$是每一层的精确程度，加权起来是$τ_w$。

另一种斜率不同的模型，可以理解为每一层先回归，再加权平均。或者把τ显式地拆开。

Model Based方法

让参数取决于新的参数（超参数）。

配对随机化试验

认为一对内的差异远远小于对间的差异。当样本量比较大的时候，认为能找到比较相近的个体。

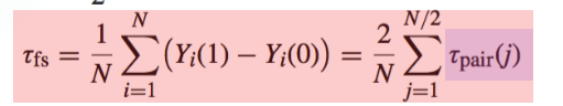
Which method can we apply straightforward?

FEP & Model-based Analysis.

主要就是其他两个要求样本量。

Fisher方法

和分层一致

Neyman方法

层内小样本的问题。

解决方法是加假设，捏合的思想：

回归方法

类似Neyman的思想。