因果推断导论笔记-Lecture7-Unconfounded Treatment Assignment & Estimating Propensity Score

观察性研究，被动地获得数据。

观察性研究下的假设

和research的关键区别是：分配机制是未知的。

满足SUTVA，W的三条假设：

1. 个体化假设

2. 随机性分配 (Probabilistic assignment)

3. 无混杂假设 (Unconfounded assignment)

   Pr(W | X, Y(0), Y(1)) = Pr(W | X)

无混杂假设

最主要的困境：无混杂假设无法先验：

而无混杂假设是不能去掉的，这会导致Simpson悖论（因为缺失数据无法直接填补）。

回归模型中隐含的无混杂假设：

所以无混杂假设是合理的，以下只探究满足SUTVA和分配机制3条假设的类型，称为ObsRAM（Regular Assignment Mechanisms）：

倾向得分

某个人群分配到处理组的概率：$e(x)=P(W_i=1|X_i=x)$

例如对于female层，看看能不能得到无偏估计。

$$\bar{Y}^{obs}_t(f)=\frac1{N_t(f)}\sum_{i:X_i=f}W_iY_i(1)$$

$$E_W[\bar{Y}^{obs}_t(f)|Y_i(0),Y_i(1),X_i=f]\\ =\frac1{N_t(f)}\sum_{i:X_i=f}E[W_iY_i(1)|Y_i(0),Y_i(1),X_i=f]\\ =\frac1{N_t(f)}\sum_{i:X_i=f}Y_i(1)E[W_i|X_i=f]\\ =e(f)·\frac1{N_t(f)}\sum_{i:X_i=f}Y_i(1)$$

核心就是 e(f) 未知。应该去估计倾向得分。

所以和分层随机化试验SRE很像，区别是$e(f)$还是$\hat{e}(f)$

Balancing Score and Propensity Score

核心思想：X可能有多个取值，找一个函数b(X)让分层降维：

证明：倾向得分是一种平衡得分。

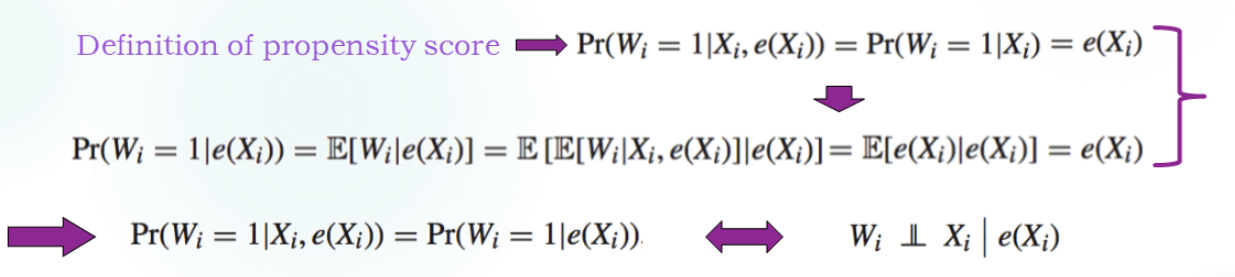
证明：倾向得分是最粗的平衡得分

也就是说倾向得分是所有平衡得分的函数。

很直观的结论。

倾向得分和分布

如果$e(x)$为常数，可以推出$X_t$和$X_c$是同分布的。

上题：已知$P(X|W_i=1)=P(X|W_i=0)$

$$e(x)=P(W_i=1|X_i=x)\\ =\frac{P(X_i=x|W_i=1)P(W_i=1)}{P(X_i=x|W_i=1)P(W_i=1)+P(X_i=x|W_i=0)P(W_i=0)}\\ =P(W_i=1)$$

也就是说e(x)是常数等价于$X_t$和$X_c$同分布。

直观理解就是竖行的比例一样，横行的X的比例是一样的。

Overview for Inference Strategies

Model-Based Imputation

可以引入贝叶斯方法，但是贝叶斯需要假设模型，产生的偏差在观察性研究中比在实验性研究中更强。特别是在协变量多的时候。

Regression Estimators

因果推断中回归模型的X的扩展是需要小心的，可能会出定义域。

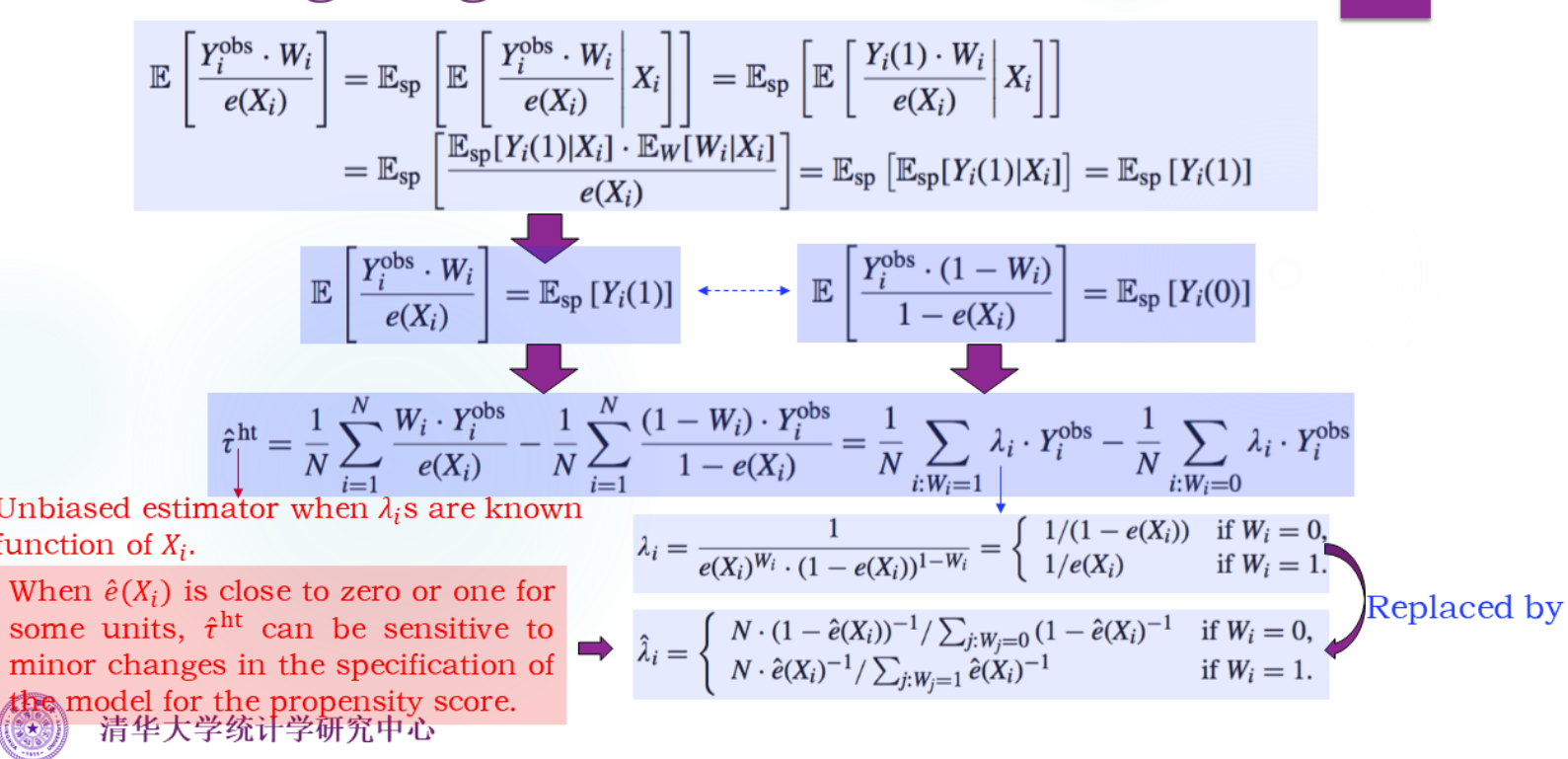
Weighting Estimators

源自Neyman的想法

Blocking Estimators

倾向得分的估计只是用于分层，不需要参与计算，所以更鲁棒。但是有偏

Matching Estimators

下节课介绍。主要是定义距离以找到匹配。

Mixed Estimators

倾向得分的重要性

在看到潜在结果前设计。

估计倾向得分是一项难点。

估计倾向得分的目的不是为了真实的倾向得分的值，而是为了后面分析：

一般采用逻辑回归来估计倾向得分。