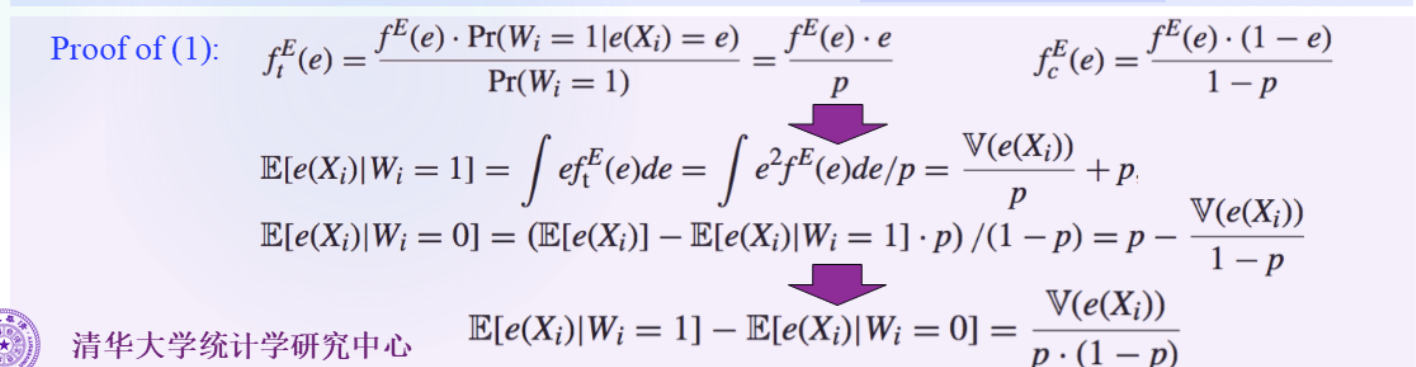因果推断导论笔记-Lecture8-Design & Analysis

理论上，哪种研究必须考察协变量的混杂性？

1. RE
2. OBS

答案：是只有OBS。问题的意思是找到某些X使得在X下W和Y独立，而随机试验中W已经是随机分配的了，已经是和Y独立了。

Design

是在看到Y之前进行的。研究W的分布。

Goal：Valid Inference

Rule：1）Inference Precision：higher、better

​ 2）Valid Range：longer、better

下面三步是一个循环。

0.估计倾向得分

见上节课。

1.Assessing Covariate Balance

How difference are the two distribution?

1. 单变量$X_i$的比较（这里的$X$应该指的是某一个维度的协变量）（优点：model free）：

2. 总体$\vec X$的比较，马氏距离（倾向得分本身就体现了协变量的重要性差异，依赖倾向得分的估计，这部分是model的）：

   

$$p=EW_i=P(W_i=1)\\ P(W_i=1|X_i=x)=E(W_i|X_i=x)=e(x)\\ 所以p=E(e(x))$$

$f_t^E(e)=f(e(X)=e|W_i=1)$

由上节课知道在e(X)下，W和X是独立的。

所以$P(W_i=1|e(X_i)=e)=P(W_i=1|e(X_i)=e,X_i=x)=P(W_i=1|X_i=x)=e(x)=e$

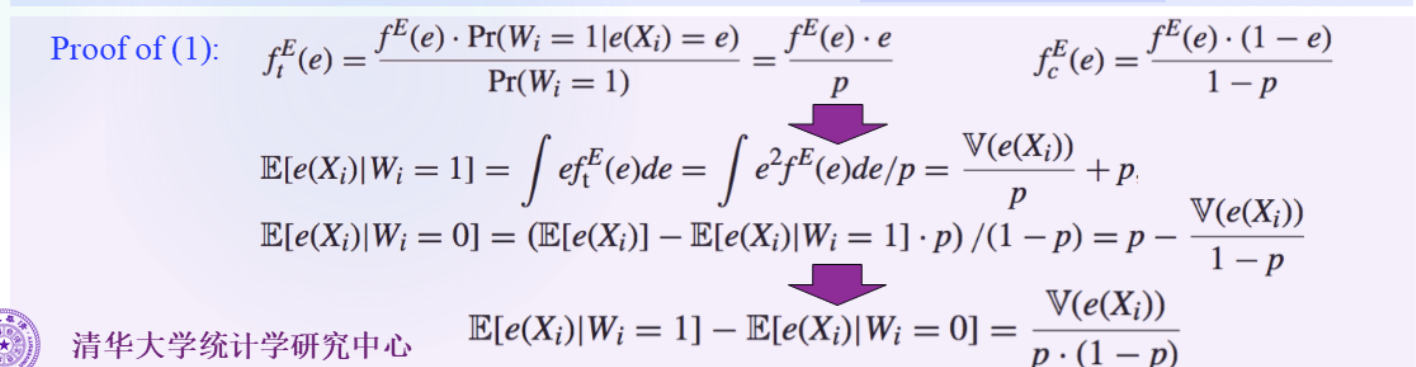
由上面的引理得到：

Whether exists similar units?

能不能找到对照？

可能要考虑舍弃一些数据。

2.Improving Balance

如果评估失败，需要平衡。

Trimming

修整：

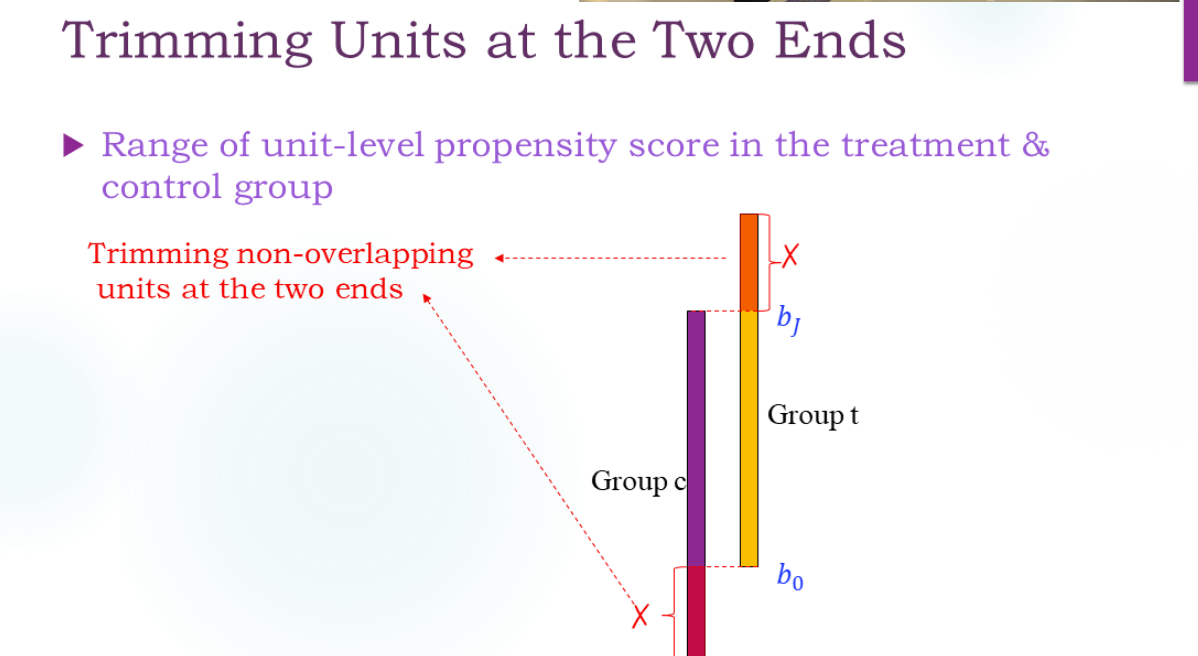
注意这里的倾向得分计算是用那个逻辑回归模型估计的，输入X得到倾向得分。

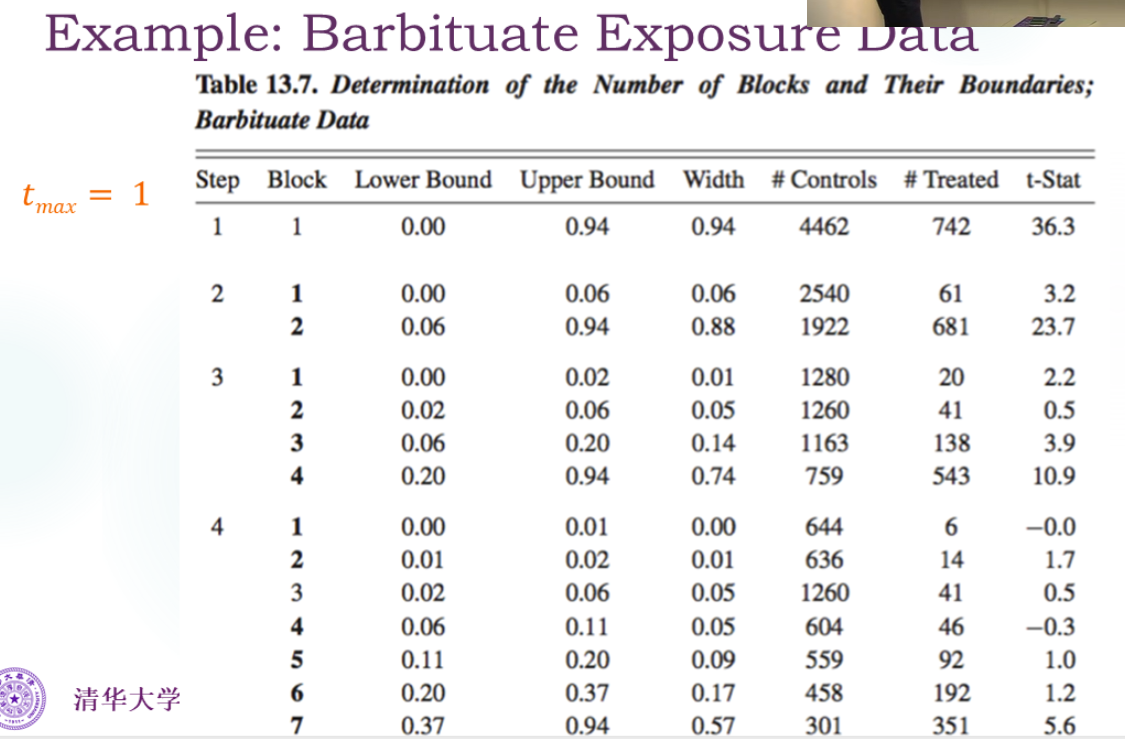
Blocking

Trimming切完之后内部也可能不均衡

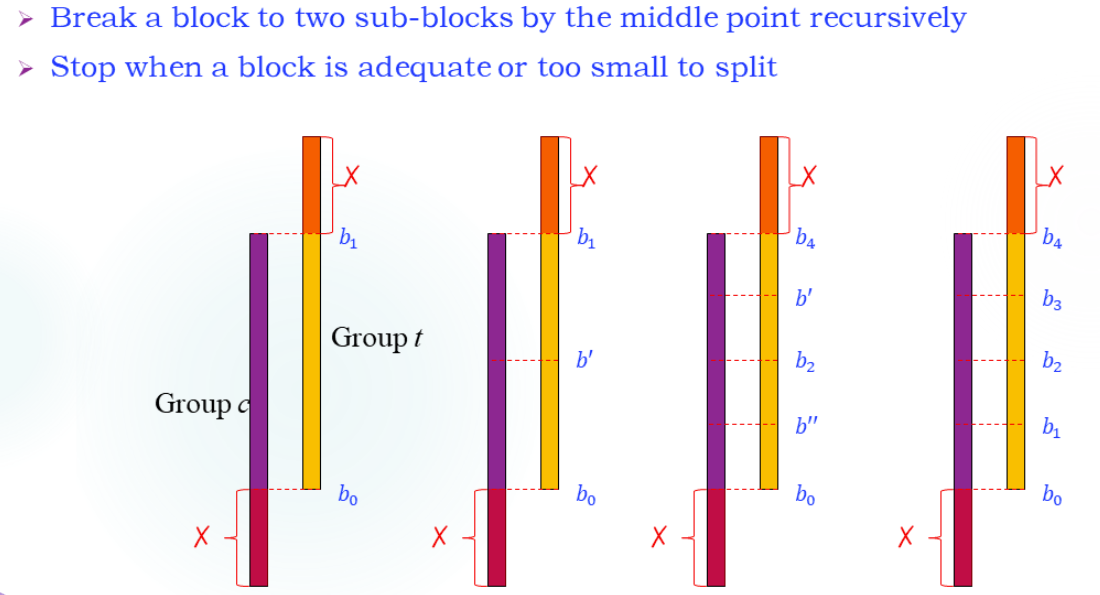
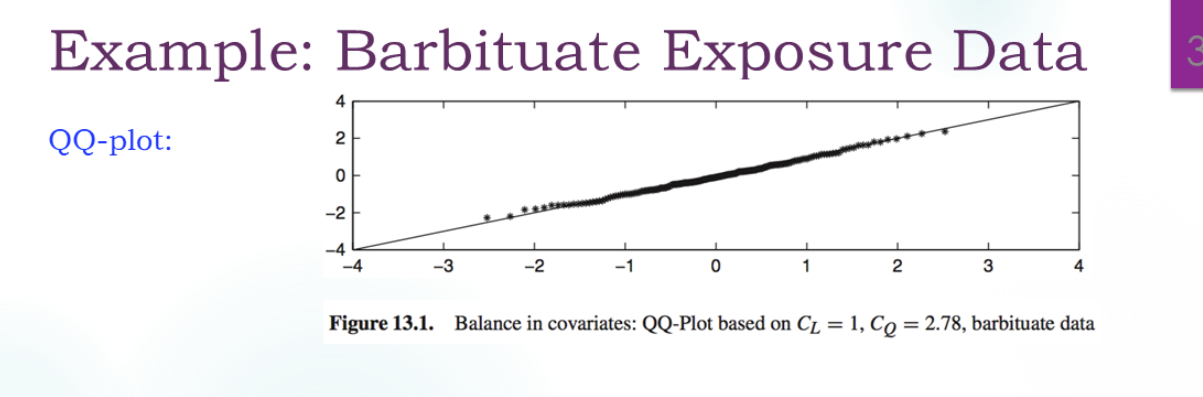
Matching

找1个相似还是M个相似，选择过程是不是无放回？（即，已经被选走的能不能被别人选走）。

Analysis

Analysis based on Blocking

blocking处理后估计的结果是不是无偏的？

期望

关心$E(\hatτ^{dif}-τ_{fs}|X)$是否为0。（简化了，不是$τ_{sp}$）

第一步第一项哪来的：

$$E(\frac{1}{N_t}\sum_{i=1}^{N}W_iY_i(1)-\frac1N\sum_{i=1}^{N}Y_i(1)|\vec X)\\ =E[E(\frac{1}{N_t}\sum_{i=1}^{N}W_iY_i(1)-\frac1N\sum_{i=1}^{N}Y_i(1)|\vec X,W)]\\ =E(\frac{1}{N_t}\sum_{i=1}^{N}W_iY_i(1)-\frac1N\sum_{i=1}^{N}Y_i(1)|\vec X,W_i=1)P(W_i=1)+\\ E(\frac{1}{N_t}\sum_{i=1}^{N}W_iY_i(1)-\frac1N\sum_{i=1}^{N}Y_i(1)|\vec X,W_i=0)P(W_i=0)\\$$

上式的第一项：

$$=E(\frac{1}{N_t}\sum_{i=1}^{N}Y_i(1)-\frac1N\sum_{i=1}^{N}Y_i(1)|\vec X)·\frac{N_t}{N}\\ =E(\frac{1}{N_t}\sum_{i=1}^{N}Y_i(1)-\frac1N\sum_{i=1}^{N}Y_i(1)|\vec X_i)·\frac{N_t}{N}\\ =\frac{N_c}{N_tN}\sum_{i=1}^{N}E(Y_i(1)|\vec X_i)·\frac{N_t}{N}\\ =\frac{N_c}{N}E(Y_i(1)|\vec X_i)$$

第二项就比较容易算了。

结果有偏（完全随机化试验下结果也一样，但这个平均差是0，所以无偏）。

分层后：

线性模型假定下：

如果真实模型不是线性模型，使用回归法调整是否还有帮助？

是。如果是高阶的$ΔY=f(ΔX)$，也能用Taylor展开。

方差

引入回归，不仅可以减少偏差，还能减少方差。（因为ε拆出了Xβ出来）

和Weighting方法的比较

也就是说Blocking是更粗的Weighting方法，用所在层的平均倾向得分e(j)来代替，而不是个体的倾向得分。

Blocking的优点就是更稳定，而Weighting是无偏的。

Analysis base on Matching

配对的顺序、配对的度量方法是很有影响的。

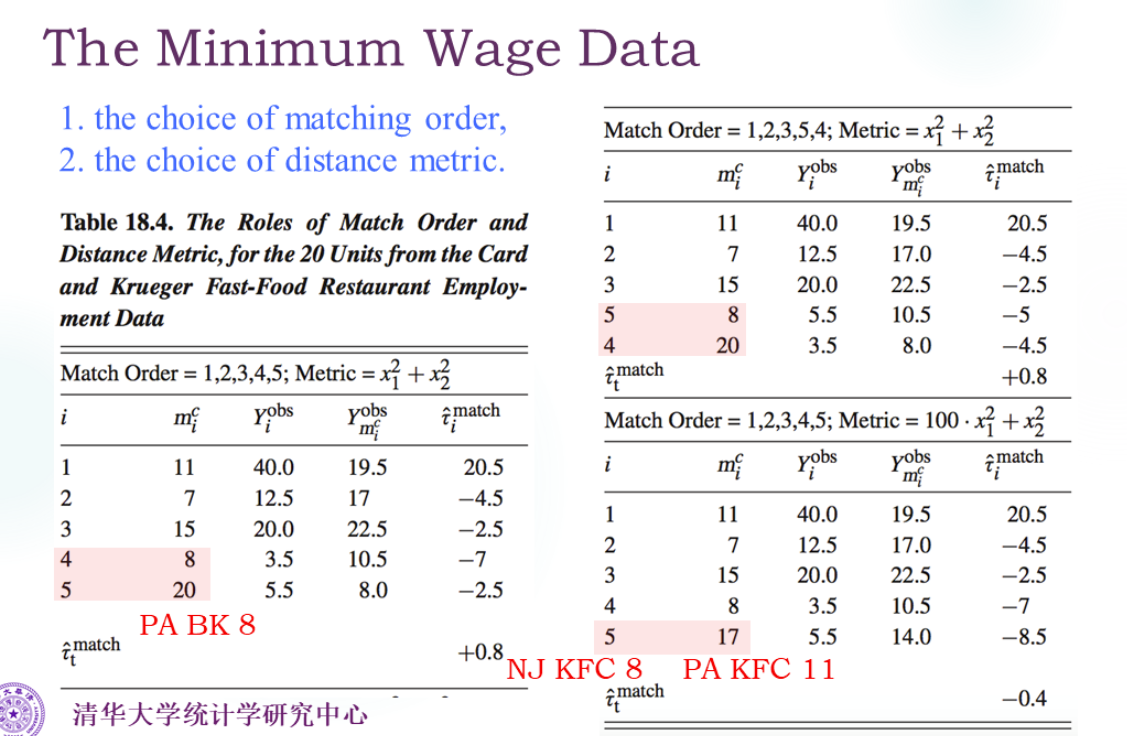
有放回的匹配：

偏差会变小，方差会变大。

反过来就是