因果推断导论笔记-Lecture9-Graphical Models-The Pearl's Framwork

图模型，新的框架。

Rubin框架的局限

X和Y都是明确的，但在很多例子中协变量、处理和结果可能都是模糊甚至是未知的。

Pearl框架

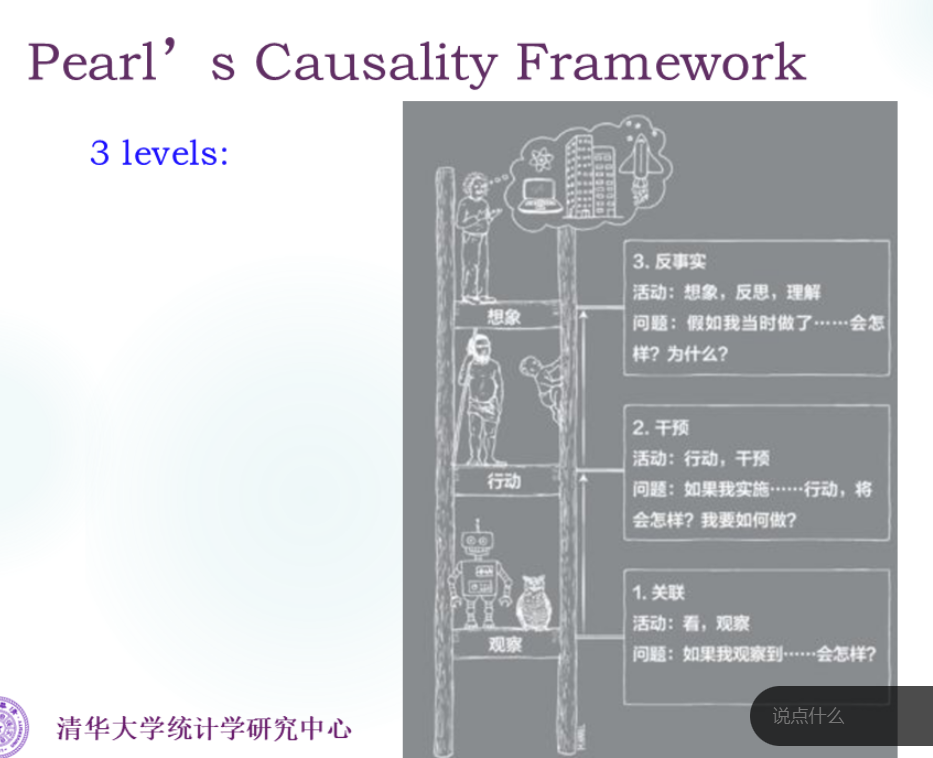
模型三要素：Graphical model（图模型）、Probability（概率）、Causality（因果）

图模型

就是离散数学的东西。

G = (V, E)

Ajacency：邻接

完全图：一对点都由一条边连接。

(Un)Directed edge、Directed graph（所有边都有向，所有边退化为无向称为骨架skeleton）

Directed acyclic graph(DAG)：有向无环图

注意这种也是DAG，环要看方向：

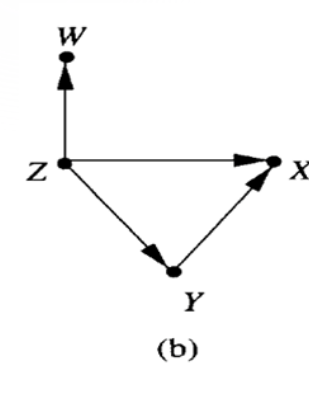
descendants后代，spouses配偶

贝叶斯网络

DAG + 概率。

概率图模型PGM

马尔可夫网络（马尔可夫随机场）= PGM with 无向图

贝叶斯网络 = PGM with 有向无环图

Rubin框架下只能从因认识结果。

引入条件独立性，减少参数

P ->拆分->G：

注意图和拆分的顺序有关，例如$P(X_2,X_1,X_3,X_4,X_5)$拆出来是$P(X_2)$在前。

蕴含同样的条件独立性，图并不是唯一的。

马氏相容性：

G ->拆分->条件独立性：

先找没有父节点的，是根节点，根节点不是条件概率。再找受它们影响的节点。

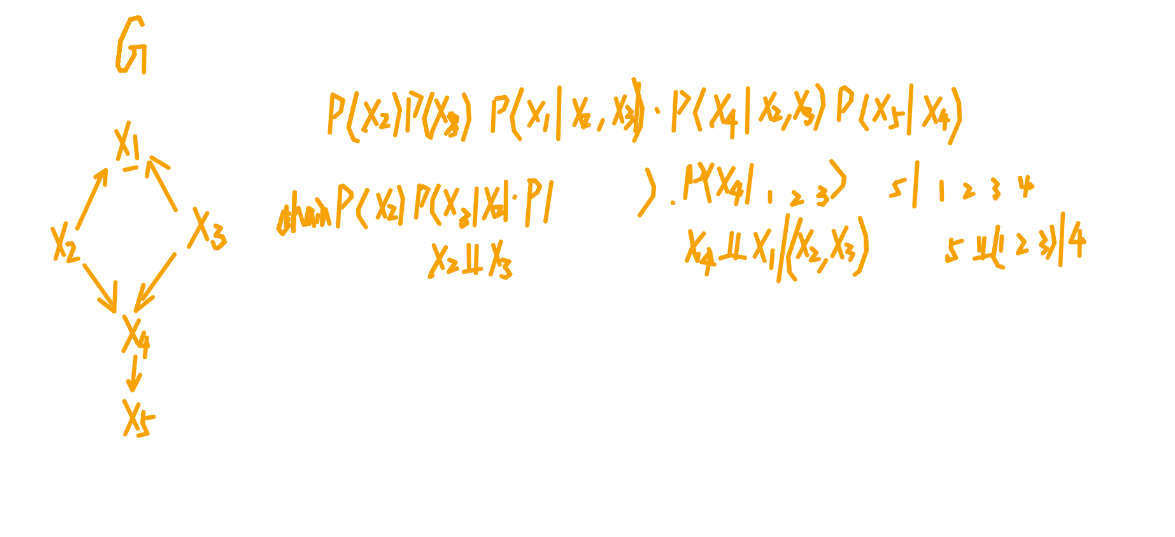
因为图只展示了定性的条件独立性，而概率还需要定量的信息。

d-separation

如何从图中直接读出条件独立性？

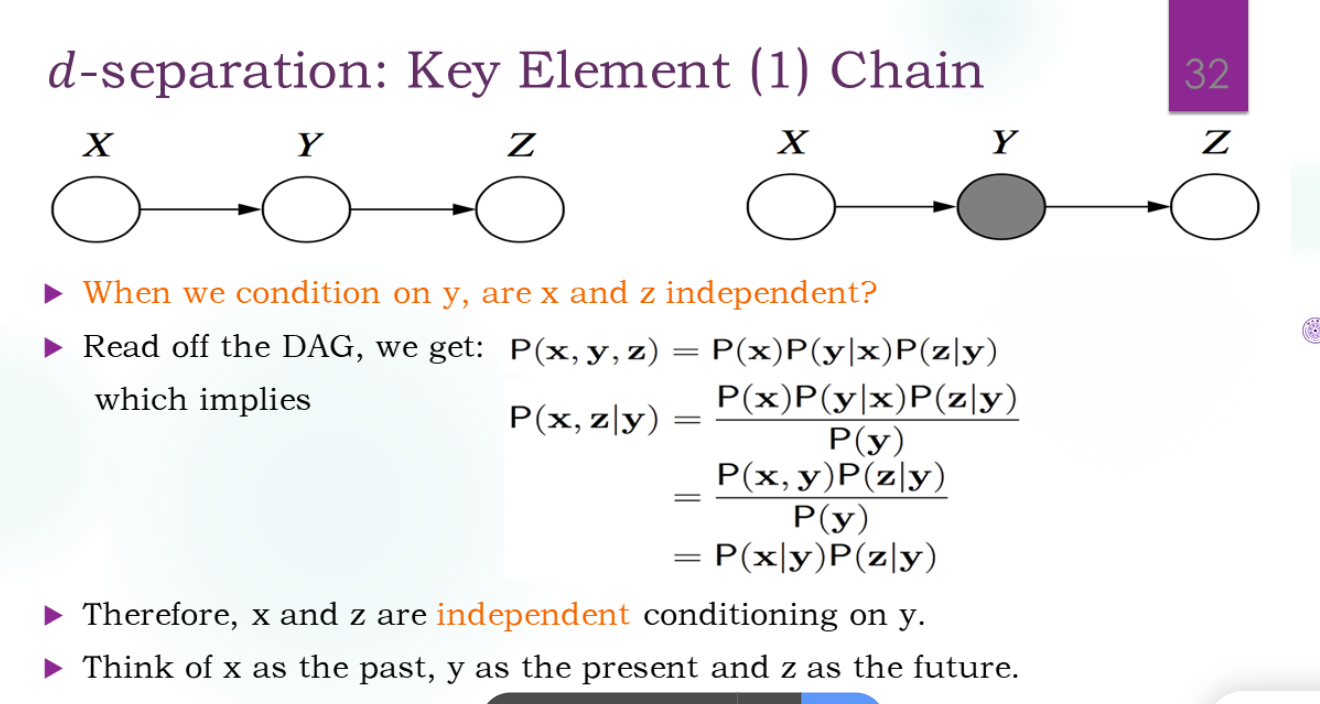
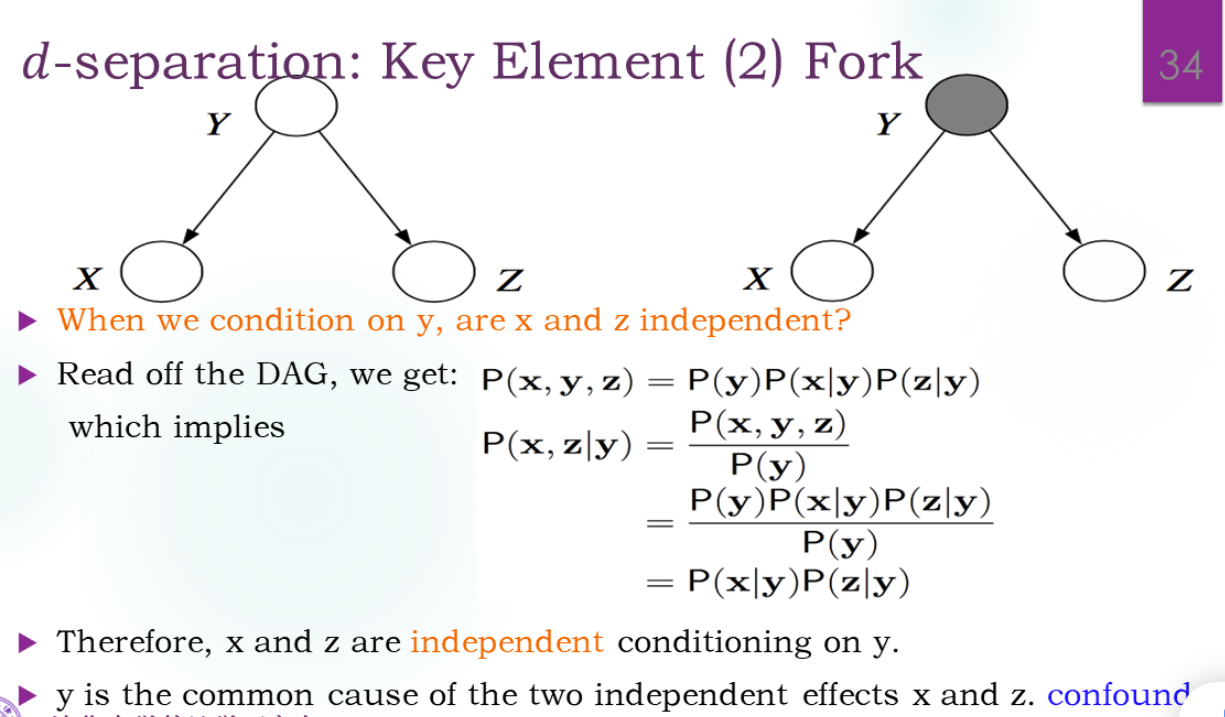
叉式法则本质上是simpson悖论，Y就是混杂的信息。

V结构，Y称为碰撞点，条件是X和Z不能存在边：

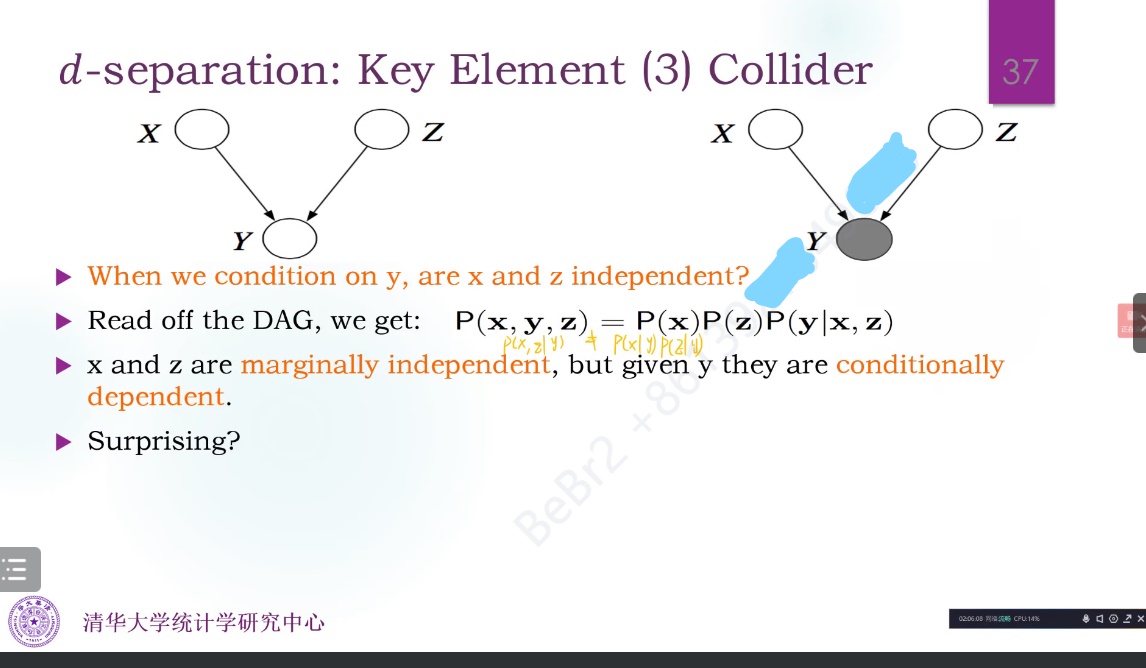
此时边缘独立，但条件却不独立了。

连续抛均匀硬币两次，X为第一次为正面，Z为第二次为正面，显然X和Z独立，定义Y为两次抛掷是否一样（一样为1），此时给定Y = 1，P(X=1, Z=1 | Y=1) = P(X=1 | Y=1) = P(Z=1 | Y=1) = 1/2说明 X|Y 和 Z|Y 不独立。

两个点下，block表示X和Z就独立了，信息不流通了。

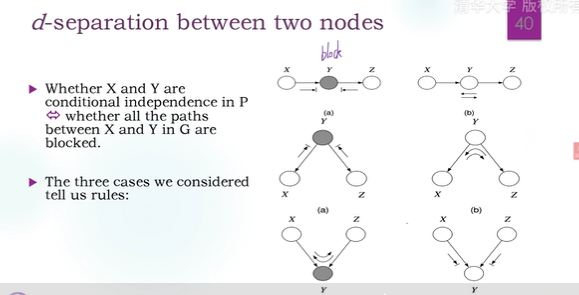
多个点的时候，链式或叉式给其中某或某几个点就可以，但不能给定V结构的碰撞点，如果非要给定碰撞点，要用其他的把那条路阻断。（给定collider的后代也不行）

也就是要把所有路都封死。

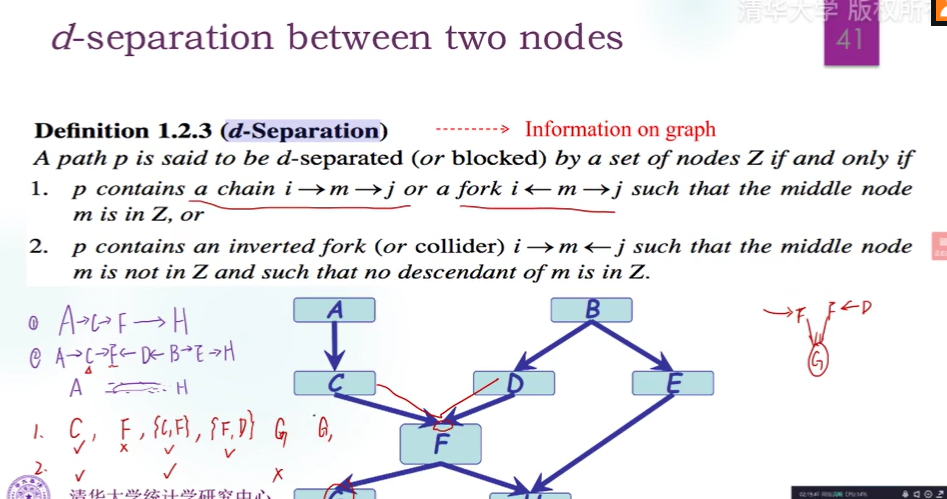
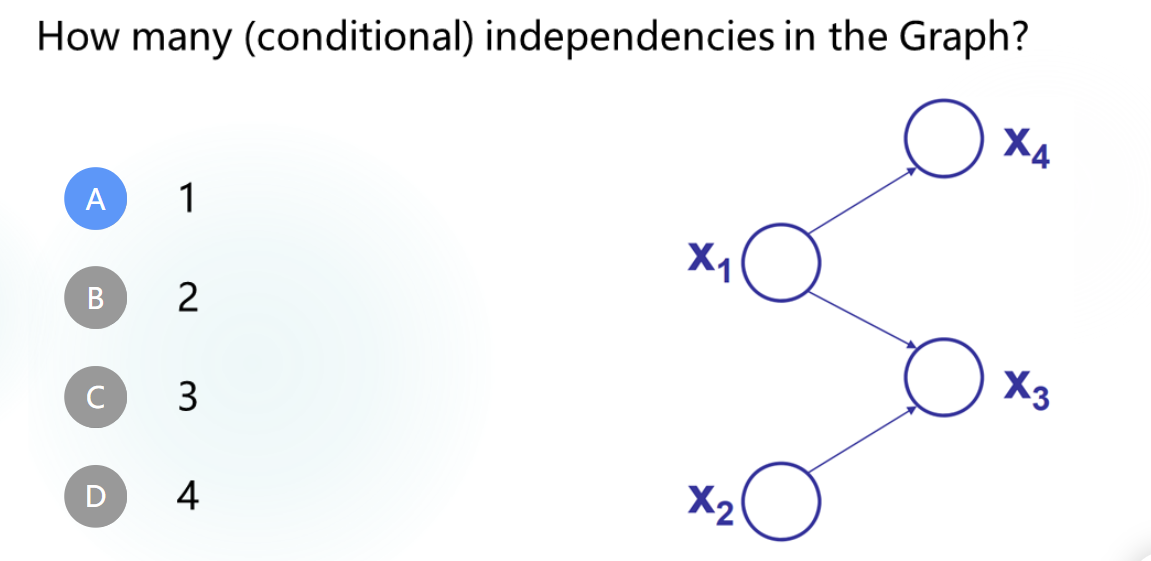
这道题问的是哪些对变量可以变成独立*（老是觉得这种判断题真的很不严谨。。。）*

做错好像是因为没看到conditional是括号（也不全是，不然应该选2）。

先通过少了哪两个点的边来关心这两个变量，看看能不能被阻断。

对于点组之间，也是类似的：