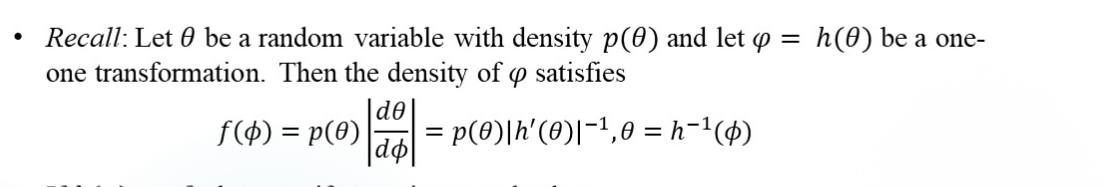三节课不学习,赶不上猫咪。(此处鸣谢new bing帮我想的这句话,略作修改。)
回顾
p(θ∣y)=p(y)p(θ,y)=p(y)p(θ)p(y∣θ)∝p(θ)p(y∣θ)
即:Posterior∝Prior∗Datalikelihood,后验正比于先验乘以似然。
先验的分类
先给一个总的表:
| Model |
Prior |
#Pre |
| Y∣θ∼B(n,θ) |
θ∼Beta(α,β) |
α+β−2 |
| Y∣θ∼P(θ) |
θ∼Γ(α,β) |
β |
| Y∣θ∼N(θ,σ2) |
θ∼N(μ0,τ02) |
τ02σ2 |
| Y∣σ2∼N(θ,σ2) |
σ2∼Inv−X2(v0,σ02) |
v0 |
Binomial Model
对于生男孩女孩的模型:
Likelihood:p(y∣θ)∝θy(1−θ)n−yPrior:p(θ)∝θα−1(1−θ)β−1,θ∼Beta(α,β)Posterior:p(θ∣y)∝θy+α−1(1−θ)n−y+β−1=Beta(θ∣α+y,β+n−y)
这样,后验均值和方差为:
E(θ∣y)=α+β+nα+yvar(θ∣y)=α+β+n+1E(θ∣y)[1−E(θ∣y)]
从后验的计算可以看出,其实就是预先多看了(α−1)个女婴,(β−1)个男婴。
引出了共轭先验的概念:
If F is a class of sampling distirbutions p(y∣θ), and P is a class of prior distributions for θ, then the class P is conjugate for F if:
p(θ∣y)∈P for ALL p(⋅∣θ)∈F and p(⋅)∈P.
均值的解释性:
E(θ∣y)=α+β+nα+y=α+β+nnny+α+β+nα+βα+βα
其实就是数据均值和先验均值的加权平均。
E(θ)=E(E(θ∣Y)):θ的先验均值其实就是所有后验分布均值的平均。
var(θ)=E(var(θ∣Y))+var(E(θ∣Y))⇒var(θ)≥E(var(θ∣Y)):后验方差平均上小于先验方差。
Poisson Model
Likelihood:p(y∣θ)∝θnyˉe−nθPrior:p(θ)∝θα−1e−βθ,θ∼Gamma(α,β)Posterior:θ∣y∼Gamma(α+nyˉ,β+n)
然后先验信息量是β的原因是,Prior中β位置和似然中n位置一样。
Normal Mean with Known Varivance
Likelihood:p(y∣θ)=2πσ1e−2σ21(y−θ)2Prior:p(θ)=eAθ2+Bθ+C即p(θ)∝e−2τ021(θ−μ0)2Posterior:θ∣y∼N(μ1,τ12)
其中,计算得到:
μ1=τ021+σ21τ021μ0+σ21yτ121=τ021+σ21
其中第二行是:后验精度=先验精度+数据精度。
当观测到多个y时,变为:
μn=τ021+σ2nτ021μ0+σ2nyˉτ121=τ021+σ2n
由数据精度的计算:σ2n可以推测,先验精度σ2n0=τ021,自然有先验样本量为σ2/τ02
预测时:
由于y~∣θ∼N(θ,σ2),θ∣y∼N(μ1,τ12),又由于y和y~独立,所以y~∣θ,y∼N(θ,σ2)。
接着,把∣y遮掉,相当于θ边缘是正态,y~∣θ是正态,且结果是θ的线性函数,所以它们的联合分布(y~,θ)也是正态,于是边缘y~是正态,最后加上条件y,就是y~∣y是正态。
(第一行,第一个是带条件的重期望,第二个是上面结论):
E(y~∣y)=E(E(y~∣θ,y)∣y)=E(θ∣y)=μ1var(y~∣y)=E(var(y~∣y,θ)∣y)+var(E(y~∣y,θ)∣y)=σ2+τ12
Normal Varivance with Known Mean
这一部分的推导有点难。直接上多个观测值的推导:
Likelihood:p(y∣σ2)∝σ−ne−2σ21∑i=1n(yi−θ)2=(σ2)−n/2e−2σ2nv其中 v=n1i=1∑n(yi−θ)2
从这个似然,想到构建共轭先验的时候,是类似于xαe−2xβ的形式。而Gamma分布是xα−1e−βx的形式,所以令z=1/x,fz(z)=f(x)z21=z−(α+1)e−zβ,称为逆Gamma分布,即Inv−Γ(α,β)。
又由Gamma和卡方的关系,Γ(v0/2,1/2)=Xv02,所以也可以找到逆卡方分布的形式。
Conjugate Prior:p(σ2)∝(σ2)−(α+1)e−σ2β可写成 p(σ2)∝(σ2)−(2v0+1)e−2σ2v0σ2
这样凑出了:
σ2∼Inv−Γ(α,β)σ2∼Inv−X2(v0,σ02)σ2=Xσ02v0,X∼Xv02
于是后验:
Posterior:σ2∣y∼Inv−X2(v0+n,v0+nv0σ02+nv)
对比一下,v0就是先验信息量,而nv是样本总方差,v0σ02就是先验总方差。
无信息先验 Non-infomative Prior
在Normal Mean with Known Variance中,如果τ02趋于无穷,相当于先验样本量为0。这个时候先验不是一个"proper distribution"(恰当的分布,简单地说就是积分为1),但后验是恰当的。这是一种得到无信息先验的办法,但并不总是有效。
无信息先验并不一定是均匀分布,例如在Normal Variance with Known Mean中,找p(σ)∝1,根据下面公式:
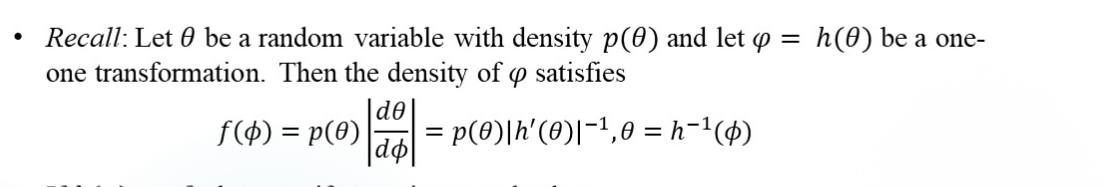
算出p(σ2)∝2σ1。
Jeffrey’s Prior
这就引出一个问题:
Can we pick a prior where the scale the parameter is measured in doesn’t matter?
答案是Jeffrey’s Prior,具有不变性:
对于参数θ,先验是pθ(θ)=π(θ),一一映射到ϕ=h(θ),先验变为pϕ(ϕ)=pθ(θ(ϕ))∣dϕdθ(ϕ)∣=η(ϕ)。Jeffery’s invariance principle能使得π(⋅)=η(⋅),也就是希望η(ϕ)=π(ϕ)。
借助了Fisher信息量(对y求期望):
J(θ)=−E(dθ2d2logp(y∣θ)∣θ)
Jeffrey’s Prior是:
p(θ)∝[J(θ)]1/2
有(推导过程略,复习时应该看一下):
J(ϕ)1/2=J(θ)1/2∣dϕdθ∣
对于Normal model with unknown variance,p(σ)∝σ1,p(σ2)∝σ21,计算p(logσ):
不能想当然地认为是logσ1,相当于f(1)=1,f(2)=21并不能说明f(3)=31(也就是说你不知道π(⋅)的形式)。应该根据Jeffrey先验的性质:
p(logσ)=p(σ)∣dlogσdσ∣∝1
Binomial Model的结论:

Pivotal Quatities枢轴量
枢轴量的分布与参数无关。
在y∼N(θ,1)的模型中,令u=y−θ,u就是一个枢轴量。
我们希望f(u∣y)∝1⋅f(u∣θ),对比p(θ∣y)∝p(θ)p(y∣θ),结合概率密度的变换公式可以算出p(θ)∝1。
例如在y∼N(0,θ2)的模型中,u=θy是枢轴量,计算出p(θ)∝θ1。