论文阅读笔记 ScatterBrain加速Transformer注意力计算

数值分析大作业我完成的部分，因为这部分涉及的证明还是花了不少时间（即使只是看论文qaq），所以记录一下。（因为自己写的一键推送脚本的某些鲁棒性不足，图片和latex公式混在一起了，呃呃）

题目	Scatterbrain: Unifying Sparse and Low-rank Attention Approximation
论文链接	https://arxiv.org/abs/2110.15343
作者单位	斯坦福
文章类型	短文

Transfomer模型的注意力机制

Transformer模型被广泛运用于自然语言处理和计算机视觉等领域，经典的Transfomer模型由encoder和decoder组成，其中均运用了注意力机制来让模型能够聚焦于输入序列中与当前位置有关的部分。一般来说，注意力矩阵的计算如下：

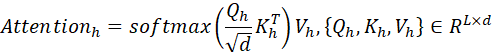
最终多头注意力的结果由上式得到的若干个注意力拼接得到。从上式可以看到，注意力层计算的时间复杂度是O(L²d)（如果忽略固定的维度大小d，就是O(L²)），主要是softmax中两个矩阵相乘需要做L²d次乘法，其中L是输入序列的长度。这种二次复杂度限制了Transformer在处理长序列任务时的性能。

问题定义

上述注意力矩阵近似的问题，可以公式化为两个目标最小化的权衡：

找到某个函数f，最小化与真实矩阵的误差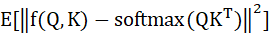同时尽量降低f的时间复杂度。

ScatterBrain近似

3.2.1 理论支撑

Scatterbrain的理论基础建立在鲁棒性主成分分析算法（Robust PCA）上。传统统计学的主成分分析一般通过样本协方差矩阵的分解（例如SVD分解或基于特征值分解）来对全局数据降维，而Robust PCA则提出了一种多项式时间的算法，试图提取数据矩阵的结构信息和噪声信息（对应的是低秩矩阵和稀疏噪声矩阵)，试图权衡低秩矩阵的秩大小和稀疏矩阵的模大小。

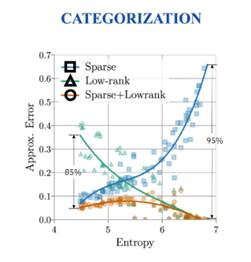
Robust PCA提供了一个思路，即数据矩阵的低秩近似和稀疏近似可能是互补的，基于此，论文作者探究了在softmax温度不同时，对注意力矩阵使用稀疏近似、低秩近似和Robust PCA的估计误差，发现Robust PCA得到的近似更准确，且低秩矩阵和稀疏矩阵的近似有互补的可能（见图）。

但是，Robust PCA的思路是从一个完整的数据矩阵分解，理论上能得到最优化的结果，但可惜我们无法提前获得注意力矩阵。Transformer注意力机制的加速要求算法从还未相乘的Q、K矩阵得到这一分解。

3.2.2 实现思路

Scatterbrain结合前人对Transformer注意力机制的低秩近似和稀疏近似的工作，提出如下近似思路：

1. 低秩近似：采用类Performer方法，使用一个随机化的核函数映射$\phi:R^d \rightarrow R^m, \phi(x)=\frac1{\sqrt{m}}exp(Wx-||x||^2/2)$，其中$W∈R^{m\times d}$，其元素独立同分布地从N(0, 1)中抽取。对于矩阵Q、K，按行使用该映射，最后得到近似矩阵$\tilde{Q}=\phi(Q)$和$\tilde{K}=\phi(K)$。

2. 稀疏近似：假设得到一个集合S，其元素是二元组$(i, j)$，构造一个稀疏矩阵M，定义如果$(i,j)∈S, M_{ij}=exp(q_i^Tk_j)-\phi(q_i)^T\phi(k_j)$，否则置为0。在实际实现中，集合S可以使用多种方法获得，例如最简单的滑动窗口模型，只有符合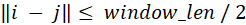才能进入集合S。Scatterbrain默认采用局部敏感哈希LSH方法，这种方法主要用于高维海量数据的快速近似查找，使用某种距离度量方式d， LSH要求哈希函数h满足如下条件：

   1. 如果d(x, y) ≤ d1， 则h(x) = h(y)的概率至少为p1；

   2. 如果d(x, y) ≥ d2， 则h(x) = h(y)的概率至多为p2；

   在Scatterbrain算法中，对于Q、K矩阵的每一行计算哈希值，落入同一个桶中的i和j才能进入支撑集S。

3. 最终Scatterbrain的近似结果（未归一化）为$\tilde{Q}(\tilde{K}^TV)+MV$。前一项使用$\tilde{Q}\tilde{K}^T$低秩近似归一化前的softmax结果，后一项则补偿误差。

可以看到Scatterbrain 具有很好的灵活性，可以使用不同的低秩近似和不同的稀疏近似组合，而不需要拘泥于上文的Performer + LSH哈希的组合。

3.2.3 无偏性与低方差

Scatterbrain不仅在时间上实现了次二次复杂度（见下文证明），而且它仍然保持了其低秩近似部分Performer的无偏性，以及更小的方差，以下的证明支持了这一点。

在未归一化的情况下，对于完全注意力机制矩阵A，有$A_{ij}=exp(q^Tk)$，其中$q,k∈R^{L\times d}$分别是第i、j个输入在Q、K矩阵里对应的向量，这里省略了通常情况的$\frac1{\sqrt{d}}$的缩放，因为可以把系数事先计算进Q或K矩阵中。对于低秩近似的版本，

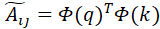
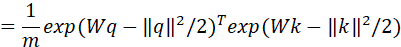
由上述定义知，$W∈R^{m\times d}$，假设W的第i行行向量为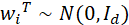那么上式可以写为：

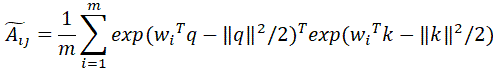
下面考虑如下期望：

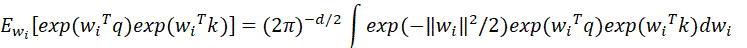
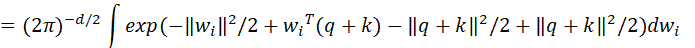
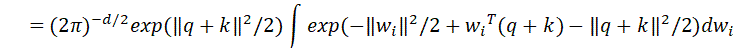
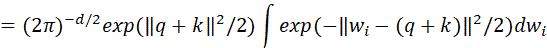
积分部分里与前面的系数组合，是多元正态分布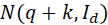的概率密度函数，所以积分结果为1，因此：

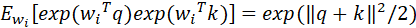
所以：

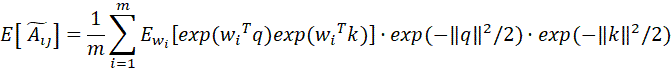
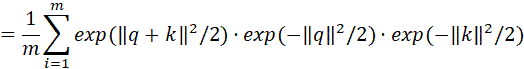
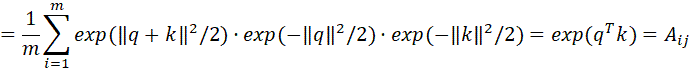
上述证明了低秩近似部分的无偏性，对于Scatterbrain得到的注意力矩阵$A^{sb}$，有如下两种情况：如果$(i,j)\notin S,A^{sb}_{ij}=\tilde{A_{ij}}$；如果$(i,j)∈S, A^{sb}_{ij}=\tilde{A_{ij}}=\phi(q)^T\phi(k)+q^Tk-\phi(q)^T\phi(k)=A_{ij}$。根据重期望公式，设示性变量$I_{(i,j)}\in S$，那么有：

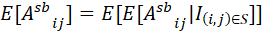
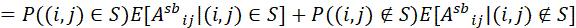
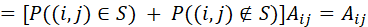
因此Scatterbrain整体的无偏性也得到了证明。

从方差角度，Scatterbrain整体的方差不大于其低秩近似部分。具体而言，根据重方差公式，有：$Var(A^{sb}_{ij})=E[Var[A^{sb}_{ij}|I_{(i,j)\in S}]]$，右式后者恒为0，因为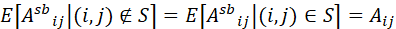所以方差为0，因此：

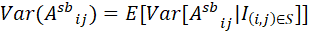
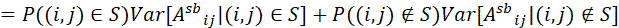
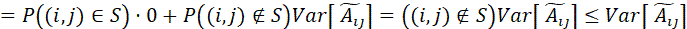
综合上述证明，可以看到Scatterbrain在继承了Performer低秩近似的优良性质的同时，还有更高的估计精确性，这是其稀疏近似支撑集S带来的。

时间复杂度分析

对于矩阵$A\in R^{a\times b},B\in R^{b\times c}$相乘，时间复杂度是$O(abc)$。因此完全注意力矩阵的计算时间复杂度是$O(L^2d)$，其中L是序列长度。

Scatterbrain之所以能降低时间复杂度，是因为其将原来必须要事先计算的$QK^T$，拆分成事先计算$\tilde{K}^TV$，因为注意力矩阵计算的二次复杂度就来源于$QK^T$。

在低秩近似阶段，核函数计算的复杂度为$O(Lmd)$，对于$\tilde{Q}(\tilde{K}^TV)$部分，复杂度也是$O(Lmd)$。对于稀疏补偿，设LSH映射的桶宽为s，那么S每一行的非零元素个数小于s，因此，复杂度不会超过$O(Lsd)$，通常s的设置小于m（例如本实验中s设置为64，m设置为128），所以总的复杂度为$O(Lmd)$。