强化学习基础

做一些强化学习的记录，以备查看，后续可能会持续更新。

基本概念

随机变量通常用大写，观测到的常量用小写。

1. Agent：可以理解为智能体。
2. State：环境的某个状态。
3. Action：Agent在某个时刻的选择。
4. Policy：记作π，定义Policy Function：$\pi(a|s)=P(A=a|S=s)$。
5. Reward：Agent做出Action后，环境返回的奖励。$R_i$取决于$S_i$和$A_i$。
6. State Transition：Agent做出Action后导致环境的State改变。可以是随机化的，如$p(s^{'}|s,a)=P(S^{'}=s|S=s,A=a)$。
7. 两个随机变量：$A\sim \pi(·|s), S^{'}\sim p(·|s,a)$
8. (state, action, reward) Trajectory：轨迹，指一次迭代（Episode）结束后，将(s, a, r)串起来：

9. Discounted Return(cumulative discounted future reward)：折扣回报，定义为$U_t=\sum_{k=t}\gamma^{k-t}R_k$，上标通常是终止时刻n。这是一个随机变量，我们能观察到的是$u_t=\sum_{k=t}\gamma^{k-t}r_k$。

   根据上式，可以推出：$U_t=R_t+\gamma U_{t+1}$。

10. Action-Value Function：动作价值函数，定义为$Q_\pi(s_t,a_t)=E[U_t|S_t=s_t,A_t=a_t]$，取决于$s_t,a_t,\pi$ 和 $p$。

11. State-Value Function：状态价值函数，定义为$V_\pi(s_t)=E_A[Q_\pi(s_t,A)]$，其中$A\sim \pi(·|s)$。评价状态s的好坏。

12. Optimal action-value function：最优动作价值函数，定义为 $Q^*(s_t,a_t)=max_\pi[Q_\pi(s_t,a_t)]$。可以根据这个函数来选择下一个Action，即在状态s下，$a^*=argmax_a Q^*(s,a)$。

13. Optimal state-value function：最优状态价值函数，定义为$V^*(s)=max_\pi V_\pi(s)$，有$V^*(s)=max_aQ^*(s,a)$（这个结论似乎有问题，因为$max_aQ^*(s,a)=max_{a,\pi}Q_\pi(s,a)$，怎么看都和左式不一样。。）。

14. Optimal advantage function：最优优势函数，定义为$A^*(s,a)=Q^*(s,a)-V^*(s)$，可以理解为判断一个动作的好坏。

15. DQN(Deep Q-Network)：希望学习$Q^*(s_t,a_t)$，使用神经网络$Q(s,a;w)$来近似它。

16. Transition：指的就是一条记录$(s_t,a_t,r_t,s_{t+1})$

17. Offline RL：离线强化学习，又称Batch RL，要求Agent只能从一个固定的数据集中学习而不能试错。

方法

Value-Based Learing

目的是拟合$Q^*(s_t,a_t)$，使用神经网络$Q(s,a;w)$来近似它。DQN是一个例子。

Policy-Based Learning

Policy Function Approximation

目的是拟合$\pi(a|s)$，使用策略网络$\pi(a|s;\theta)$。

State-Value Function Approximation

目的是拟合$V_\pi(s_t)$。有$V(s;\theta)=\sum_a\pi(a|s;\theta)·Q_\pi(s,a)$。

基于策略的学习，目标是最大化$J(\theta)=E_S[V(S;\theta)]$，所以使用梯度上升来更新$\theta$。

策略梯度Policy gradient的推导就不赘述了，结果是：$\frac{\partial V(s;\theta)}{\partial \theta}=E_{A\sim \pi(·|s;\theta)}[\frac{\partial log \pi(A|s;\theta)}{\partial \theta}·Q_{\pi}(s,A)]$，这个期望可以用随机抽取一个 $\hat a$ 来近似。

算法的更新如下：

1. 观测到状态$s_t$
2. 根据策略网络$\pi(a|s;\theta)$来随机抽样$a_t$。
3. 计算$q_t=Q_\pi(s_t,a_t)$。
4. 计算$d_{\theta,t}=\frac{\partial log \pi(a_t|s_t;\theta)}{\partial \theta}|_{\theta=\theta_t}$
5. 更新网络$\theta_{t+1}=\theta_t+\beta·q_t·d_{\theta_t}$。

上述存在一个问题，第三步所用到的动作价值函数其实是未知的，有两种做法，第一种是直接做完一次迭代，使用得到的trajectory得到的$r_i$序列来估计$u_t$，然后直接令$q_t=u_t$。

另一种就是用一个神经网络来拟合$Q_\pi(s_t,a_t)$，其实就是下面的：

Actor-Critic Methods

Actor就是策略网络$\pi(a|s;\theta )$，Critic就是价值网络$q(s,a;w)$。更新的过程如下：

1. 观测状态$s_t$，采样$a_t\sim \pi(·|s_t;\theta_t)$
2. 执行$a_t$，获得环境返回的$s_{t+1}$和$r_t$
3. 随机采样$\tilde a_{t+1}\sim \pi(·|s_{t+1};\theta_t)$，但不执行这个动作，只是用来计算TD target
4. 使用价值网络计算$q_t=q(s_t,a_t;w_t)$，$q_{t+1}=q(s_{t+1},\tilde a_{t+1};w_t)$
5. 计算TD error：$δ_t=q_t-(r_t+\gamma·q_{t+1})$
6. 计算$d_{w,t}=\frac{\partial q_t}{\partial w}|_{w=w_t}$
7. 更新价值网络参数：$w_{t+1}=w_t-\alpha·δ_t·d_{w,t}$。
8. 计算$d_{\theta,t}=\frac{\partial log \pi(a_t|s_t;\theta)}{\partial \theta}|_{\theta=\theta_t}$
9. 更新策略网络参数：$\theta_{t+1}=\theta_t+\beta·q_t·d_{\theta_t}$。

算法相关

TD-Learning

核心思想就是认为下一步的估计更精确，用它作为target，以避免需要完成一次episode。

直接看Train DQN using TD Learning：

做了很多近似，得到：$Q(s_t,a_t;w)≈E[R_t+\gamma Q(S_{t+1},A_{t+1};w)]$

所以设置TD Target：$y_t=r_t+\gamma Q(s_{t+1},A_{t+1};w)=r_t+\gamma· max_a[Q(s_{t+1},a;w)]$，

就可以计算Loss了：$L_t=\frac12[Q(s_t,a_t;w)-y_t]^2$，

梯度下降：$w_{t+1}=w_t-\alpha·\frac{\partial L_t}{\partial w}|_{w=w_t}$。

整个过程如下：

1. 观测状态$s_t$，做出动作$a_t$；
2. 用Q预测价值$q_t$；
3. 计算$d_t=\frac{\partial q_t}{\partial w}|_{w=w_t}$。
4. 环境返回新的状态$s_{t+1}$和奖励$r_t$。
5. 计算TD Target $y_t$。
6. 梯度下降，更新参数：$w_{t+1}=w_t-\alpha·(q_t-y_t)·d_t$。

Sarsa算法

State-Action-Reward-State-Action，是TD-Learning的一种。

它的TD target为$y_t = r_t+\gamma·q(s_{t+1},a_{t+1};w)$

TD error为$δ_t=q(s_t,a_t;w)-y_t$。

上述Actor-Critic Methods中的TD部分就是使用Sarsa。

Q-Learing算法

最大的区别就是TD target为$y_t = r_t+\gamma·max_a[q(s_{t+1},a;w)]$，上述DQN的TD部分就是使用Q-Learing。

Multi-Step TD Target

其实就是多迭代几步，有$U_t=\sum_{i=0}^{m-1}\gamma^i·R_{t+i}+\gamma ^m·U_{t+m}$。

Experience Replay 经验回放

解决两个问题：

1. 一条Transition用完后就丢掉了，但其实是可以继续用的，主要是因为$s_t, a_t$之后，$r_t,s_{t+1}$是确定的（或者至少抽样分布是确定的）。和网络无关。
2. 相关性：相邻两条Transition有相关性，是有害的。

使用一个replay buffer，储存最近n条transitions，然后更新网络使用SGD(Stochastic gradient descent 随机梯度下降)的方法，随机在buffer里抽取一条来更新现在的网络，注意在不同时刻，相同的transition计算得到的TD error一般也是不同的，因为网络更新了。

采样方法可以让$δ$更大的以更大的概率被抽到，相应的学习率调小。例如：

$p_t \propto |δ_t|+\epsilon$ 或 $p_t\propto \frac1{rank(t)}$，其中rank为δ排名；学习率为$\alpha·(np_t)^{-\beta}$。

Target Network & Double DQN

原始的DQN对动作价值的估计是高估（overestimate）的：

1. The maximization：

   真正的action-values：$x(a_1),...,x(a_n)$

   DQN的估计是有噪声的：$Q(s,a_1;w),...,Q(s,a_n;w)$，

   当然是无偏的：$mean_a(x(a))=mean_a(Q(s,a;w))$

   但由于QLearning选取了最大的Q，有：$max_a(x(a))≤E[max_a(Q(s,a;w))]$

   ，也就是期望而言，一直是高估的。而且主要是高估是不均匀的，因为transition占比越高，高估越严重。

2. Bootstrapping自举：

   大概是由于上述高估了，然后梯度更新是自举的，导致越来越严重。

Target Network

使用另一个结构相同的DQN：$Q(s,a;w^-)$，参数每隔一段时间更新，可以是：$w^-=w$或$w^-=\tau w+(1-\tau)w^-$。

然后在算TD target时，$y_t=r_t+\gamma·max_a(Q(s_{t+1},a;w^-))$，

TD error：$δ_t=Q(s_t,a_t;w)-y_t$。

可以部分解决自举。

Double DQN

和Target Network的区别是select时使用的是主DQN的网络，即：

$a^*=argmax_aQ(s_{t+1},a;w)$

$y_t=r_t+\gamma·Q(s_{t+1},a^*;w^-)$

可以减弱高估，因为：$Q(s_{t+1},a^*;w^-)≤max_aQ(s_{t+1},a;w^-)$。

Dueling Network

容易证明$max_aA^*(s,a)=0$（根据上面那个我觉得“有问题”的结论），那么有$Q^*(s,a)=V^*(s)+A^*(s,a)=V^*(s)+A^*(s,a)-max_aA^*(s,a)$。

所以可以搭建一个Dueling Network：

$Q(s,a;w^A,w^V)=V(s;w^V)+A(s,a;w^A)-max_aA(s,a;w^A)$，

训练的时候和DQN一样就行了。其实后面减掉max只是为了唯一性，防止V和A变化导致Q不变。所以上述“有问题”的结论也不影响。

网络结构如下：

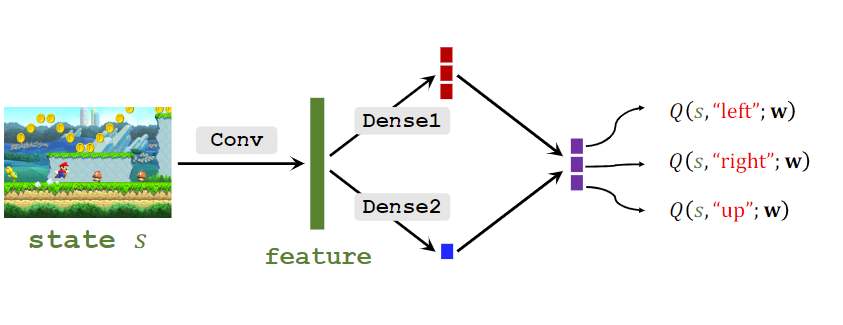
REINFORCE with baseline

这里的baseline的定义为和随机变量A独立的b。

可以证明$E_{A\sim \pi}[b·\frac{\partial ln\pi(A,s;\theta)}{\partial \theta}]=0$。

所以策略梯度可以变成：$\frac{\partial V(s;\theta)}{\partial \theta}=E_{A\sim \pi(·|s;\theta)}[\frac{\partial log \pi(A|s;\theta)}{\partial \theta}·(Q_{\pi}(s,A)-b)]$。选择合适的b可以使蒙特卡洛近似的方差更小，而保持无偏。通常选择为$V_\pi(s)$。

令策略梯度为：$g(A_t)=\frac{\partial V(s_t;\theta)}{\partial \theta}=E_{A_t\sim \pi(·|s_t;\theta)}[\frac{\partial ln \pi(A_t|s_t;\theta)}{\partial \theta}·(Q_{\pi}(s_t,A_t)-V_\pi(s_t))]$

做几层近似：$\frac{\partial V(s_t)}{\partial \theta}≈g(a_t)≈\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}·(u_t-v(s_t;w))$，

第一个约等于号是蒙特卡洛近似，随机抽样一个动作，第二个约等于号使用$u_t=\sum_{i=t}^n\gamma^{i-t}r_i≈Q_\pi(s_t,a_t)$，以及用价值网络近似V函数。

结构图如下：

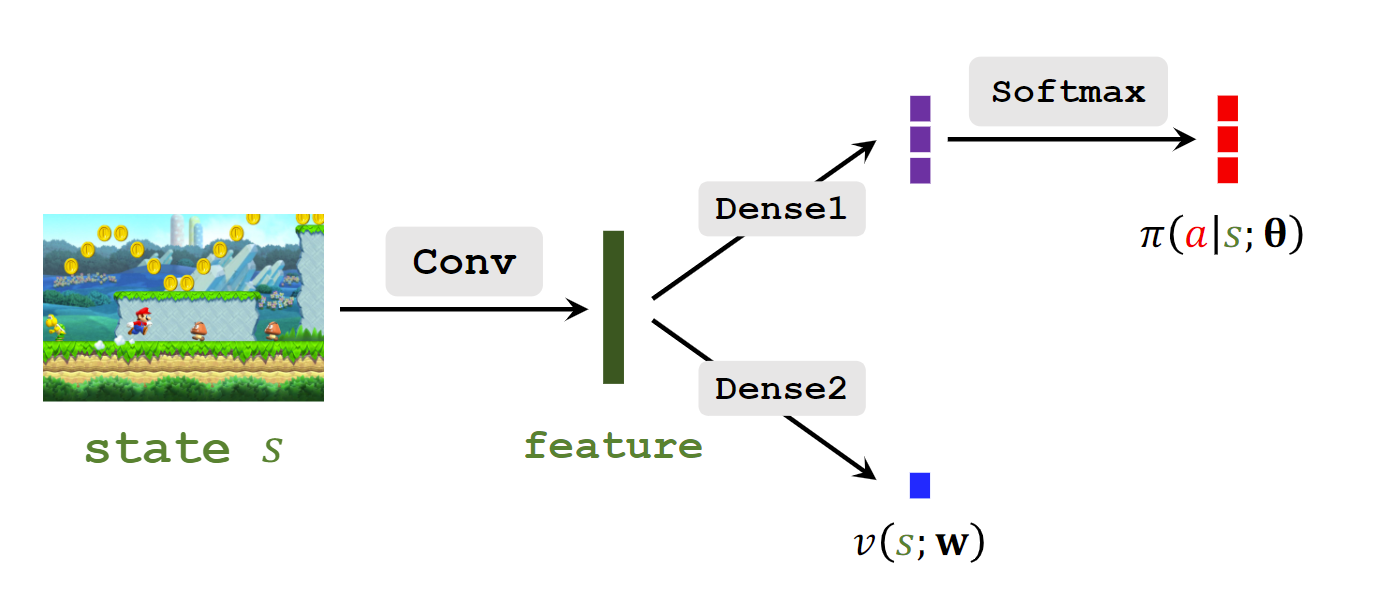
过程如下：

1. 玩完一局游戏得到trajectory；
2. 计算$u_t=\sum_{i=t}^n\gamma^{i-t}r_i$ 和 $\delta_t=v(s_t;w)-u_t$
3. 更新策略网络：$\theta = \theta-\beta ·\delta_t·\frac{\partial ln\pi(a_t|s_t;\theta)}{\partial \theta}$（注意这是梯度上升，只是δ定义的问题）
4. 更新价值网络：$w = w-\alpha·\delta_t·\frac{\partial v(s_t;w)}{\delta w}$
5. 上述过程重复n次，n为游戏完成时的时刻。

Advantage Actor-Critic (A2C)

和AC差不多，只是Critic改成了价值网络$v(s;w)$。网络结构图和REINFORCE with baseline没有区别。

TD target：$y_t=r_t+\gamma·v(s_{t+1};w)$

TD error：$δ_t=v(s_t;w)-y_t$

更新策略网络（Actor）：$\theta = \theta-\beta ·\delta_t·\frac{\partial ln\pi(a_t|s_t;\theta)}{\partial \theta}$

更新价值网络（Critic）：$w = w-\alpha·\delta_t·\frac{\partial v(s_t;w)}{\delta w}$

上述的合理性来源于如下两个结论：

1. $Q_\pi(s_t,a_t)≈r_t+\gamma·V_\pi(s_{t+1})$
2. $V_\pi(s_t)≈E_{A_t,S_{t+1}}[R_t+\gamma·V_\pi(S_{t+1})]$

将上述代入$g(a_t)$得到$g(a_t)≈\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}(r_t+\gamma·v(s_{t+1};w)-v(s_t;w))$。

和REINFORCE with baseline的区别是，REINFORCE with baseline使用了价值网络只是用于baseline，没有用于TD target，而A2C的TD target是价值网络和回报的混合。

具体来说，对于A2C with Multi-Step TD target，$y_t=\sum_{i=0}^{m-1}\gamma^i·r_{t+i}+\gamma ^m·v(s_{t+m};w)$，而REINFORCE with baseline是它的特例，直接把m - 1设置成n，后面一项就直接丢掉了。

Trust Region Policy Optimization (TRPO)

置信域算法：

1. Approximation: 给出$\theta_{old}$，寻找一个函数L，在邻域$N(\theta_{old})$内近似于 J。
2. Maximization: 在置信域$N(\theta_{old})$内，找到 L 的最大值对应的 θ 来更新参数。

应用在基于策略的强化学习中：

由于

$$J(\theta)=E_S[V_\pi(S)] \\ =E_S[E_A[\frac{\pi(A|S;\theta)}{\pi(A|S;\theta_{old})}·Q_\pi(S,A)]]$$

所以Approximation这一步可以这样做：

首先得到一个trajectory，蒙特卡洛近似：

$$L(\theta|\theta_{old})=\frac1n\sum_{i=1}^{n}\frac{\pi(a_i|s_i;\theta)}{\pi(a_i|s_i;\theta_{old})}·Q_\pi(s_i,a_i))$$

后面的Q可以用$u_i$近似，这就完成了估计。

在Maximization这一步，可以选择邻域为$||\theta-\theta_{old}||<Δ$，也可以选择其他（如KL散度约束等）。

整个过程如下：